Las Relaciones Alométricas entre la Fuerza Explosiva de los Miembros Inferiores y el Rendimiento en las Pruebas de Capacidades Físicas
Mayara M. Batista1,2, Karina A. Lopes1, Marcos R. Queiroga3, Leonardo A. Peyré-Tartaruga4, Marcus P. Tartaruga1,2,3,41 Laboratorio de Biomecánica, UNICENTRO, Guarapuava, Brasil
2 Posgrado de Educación Física, UFPR, Curitiba, Brasil
3 Escuela de Educación Física, UFRGS, Porto Alegre, Brasil
4 LAMHES, Universidad de Niza Sophia Antipolis, Niza, Francia
Resumen
Este estudio examinó las relaciones alométricas entre la fuerza muscular (S) del miembro inferior de un sujeto y su rendimiento en pruebas de capacidad física. Veinticuatro corredores recreativos (12 hombres, edad: 31 ± 7 años, masa: 78,5 ± 11,2 kg; 12 mujeres, edad: 31 ± 6 años, masa: 56,5 ± 4,4 kg) realizaron una contracción isométrica voluntaria máxima del cuádriceps, dos pruebas pliométricas, una prueba de agilidad, una prueba submáxima en cinta caminadora y una prueba de 5 km. Se determinaron los exponentes alométricos específicos para el torque y la fuerza, asumiendo la relación S = k.mb (hombre, b = 0,56 y 0,55; mujer, b = 0,48 y 0,50, respectivamente). Se observaron relaciones más fuertes entre la S dinámica y el rendimiento en las pruebas pliométricas (squat jumps - SJ, hombre, r = 0,70 y 0,80, mujer, r = 0,72 y 0,74; counter movement jumps - CMJ, hombre, r = 0,70 y 0,76, mujer, r = 0,62 y 0,63, normalización tradicional y alométrica de S, respectivamente) y de agilidad (SJ, hombre, r = 0,62 y 0,74, mujer, r = 0,65 y 0,66; CMJ, hombre, r = 0,53 y 0,66, mujer, r = 0,62 y 0,63) cuando la S se normalizó alométricamente demostrando que los aspectos morfológicos individuales son los principales determinantes del rendimiento motor. El método de escala alométrica se puede emplear para ajustar la S para el tamaño corporal y predecir las capacidades físicas de los corredores recreativos en función de parámetros fisiológicos y biomecánicos individuales.
Palabras Clave: Masa Corporal, Fuerza Muscular, Escala de Tasa Metabólica
INTRODUCCIÓN
La fuerza muscular (S) (es decir, la fuerza voluntaria máxima (F) o el torque (T) ejercido bajo condiciones mecánicas estandarizadas) a menudo se mide en diversos campos de las ciencias relacionadas con el movimiento humano. Uno de los problemas asociados con la presentación de los datos de la S es tener en cuenta el efecto de las dimensiones del cuerpo en el rendimiento. Por lo tanto, las comparaciones de la S medida ajustadas para la masa corporal (m) u otras variables de tamaño corporal, en lugar de comparaciones de S absoluta, generalmente se usan en todo el ejercicio, el deporte y la bibliografía de las ciencias médicas (9,23).
Por lo general, se han aplicado dos métodos para ajustar la S al tamaño corporal. El primer método requiere el cálculo de los llamados estándares de ratio, para los cuales la S por unidad de tamaño corporal se obtiene al dividir S por m (12). El segundo método, de escala alométrica, se basa en un principio propuesto por Rubner (36), que generalmente se conoce como similitud geométrica o biológica (43), y se ha aplicado recientemente en ciencias de la salud o ciencias del movimiento humano (31). Este método corresponde a una ecuación de regresión (Y=k.mb) que indica el comportamiento de la variable fisiológica Y (por ej., S) en m, donde k corresponde a la intercepción vertical, llamada coeficiente alométrico (característica constante para el organismo), y b es el exponente alométrico o de escala (23,40). Cuando b es igual a 1, la relación es isométrica y cuando no lo es, la relación es alométrica. La función exponencial se puede transformar en una función lineal de la siguiente manera: log Y = log k + b log m.
La evaluación de las capacidades físicas es uno de los problemas más importantes en diversos deportes y muchas pruebas se utilizan para guiar los procedimientos de selección, examinar a los candidatos o controlar la eficacia de los protocolos de entrenamiento (32). Los estudios existentes que han examinado la S y la potencia de los miembros inferiores con frecuencia utilizan la prueba isocinética de rodilla y la prueba de salto vertical. Por ejemplo, Alemdaroglu (1) y Cronin y Hansen (11) no determinaron ninguna relación entre la S de extensión y flexión de rodilla y el rendimiento del sprint simple. Sin embargo, por otro lado, Dowson et al. (13) encontraron una relación estadísticamente significativa entre los torques concéntricos y excéntricos de los extensores de rodilla y los tiempos de carrera de 0 a 15 m y de 30 a 35 m. De manera similar, Alexander (2) encontró una fuerte correlación entre el rendimiento del sprint, el mejor tiempo de sprint personal de 100 m y el torque concéntrico de extensión de rodilla, en 4,14 rad·s-1, en los velocistas de elite.
Una explicación razonable de la falta de correlación entre la S isocinética de rodilla y el rendimiento del sprint simple podría deberse a una serie de diferencias en el enfoque del estudio, como las variaciones en las velocidades angulares articulares y la posición de los sujetos, lo que podría afectar la longitud y velocidad de contracción, las características del sujeto y métodos utilizados para calcular la producción de potencia de la articulación en el dinamómetro isocinético (20). La falta de asociación también podría atribuirse a las características particulares de los sujetos involucrados en los respectivos estudios. Se reconoce ampliamente que, si bien el método de escala alométrica implica que la S aumenta a una velocidad menor que m (es decir, S por kilogramo2/3 es el ajuste correcto para m), el estándar de ratio supone que S aumenta proporcionalmente a m (es decir, S por kilogramo1 es el ajuste correcto para m) (23). Dado que la S representa una variable fisiológica importante en varias ciencias relacionadas con el movimiento, Davies y Dalsky (12) y Neder et al. han probado y discutido recientemente ambos métodos (29). Sin embargo, a pesar de estos esfuerzos, el método óptimo para ajustar la S a las diferencias en el tamaño corporal aún permanece abierto a discusión (23). Además, a pesar de los pocos estudios, las capacidades físicas parecen estar mejor expresadas por exponentes alométricos y, debido a su importancia inherente para las actividades deportivas de la vida diaria, estos cálculos abren un enfoque útil y mejorado para evaluar los parámetros motores funcionales.
El propósito de este estudio fue investigar las relaciones alométricas entre la fuerza muscular explosiva de los miembros inferiores y las pruebas de rendimiento de salto y agilidad. Se generó la hipótesis de que el método de escala alométrica se puede utilizar para ajustar la S al tamaño corporal y predecir las capacidades físicas de los corredores recreativos, basándose en el suministro límite individual y/o los procesos fisiológicos que contribuyen a la regulación de la tasa metabólica y respuestas neuromusculares, demostrando una relación morfofuncional no lineal.
MÉTODOS
Sujetos
Un total de 24 corredores recreativos (12 hombres y 12 mujeres) sin problemas ortopédicos, neuromusculares o cardiovasculares conocidos se ofrecieron como voluntarios para participar en esta investigación. El tamaño de la muestra se calculó utilizando el programa PEPI (J.H. Abramson y P.M. Gahlinger, Computer Programs for Epidemiologists: PEPI versión 4.0; Sagebrush Press, Salt Lake City, UT, EEUU) con una potencia del 90% para cada variable. Los sujetos leyeron y firmaron un formulario de consentimiento antes de participar en el estudio, que fue aprobado por el Comité Institucional de Ética e Investigación de la universidad local (n°: 344.468). Todos los procedimientos experimentales se llevaron a cabo de acuerdo con el código de ética de la Asociación Médica Mundial (Declaración de Helsinki). Se registró el rendimiento de la prueba de 5 km contrarreloj en competiciones regionales realizada entre 2 y 5 semanas antes del período de evaluación para caracterizar a los sujetos. En esta distancia, del 10 al 12% de la energía total producida se traduce en una contribución anaeróbica, importante en el rendimiento de carrera de media distancia.
Procedimientos
Los sujetos se sometieron a una sesión experimental de laboratorio que se dividió en tres partes: (a) caracterización de la muestra y prueba submáxima de carrera en cinta caminadora; (b) contracción isométrica voluntaria máxima de cuádriceps y pruebas pliométricas; y (c) prueba de agilidad (Figura 1). Debido a la influencia del medio ambiente en los procesos fisiológicos que contribuye a la regulación de la tasa metabólica y respuestas neuromusculares, la temperatura ambiente del laboratorio (25°C) y la humedad relativa (53%) se controlaron de acuerdo con ISO-8573-1 (normas internacionales). Se impusieron varias restricciones a los sujetos: (a) sin alimentos y bebidas al menos 3 a 4 horas antes de las pruebas; y (b) sin estimulantes o actividad física intensa 12 horas antes de la evaluación.
Parte 1: Caracterización de la Muestra y Prueba Submáxima en Cinta Caminadora
Los parámetros antropométricos se registraron usando balanzas y un estadiómetro "Filizola" (Modelo 31, São Paulo, Brasil), un plicómetro "Lange Skinfold Caliper" (Modelo C-130, Cambridge, EEUU) y un "Lufkin" antropométrico (Modelo W606PM, Ohio, EEUU) (24). El porcentaje de grasa corporal se calculó usando la ecuación de Siri (38). La densidad corporal se calculó utilizando el método de Jackson y Pollock (21). Después de tomar las medidas antropométricas, cada sujeto realizó una prueba submáxima en una cinta caminadora "Movement" (Modelo RT350, São Paulo, Brasil) para evaluar el consumo voluntario de oxígeno, conocido también como VO2máx, una variable importante para la caracterización de la muestra. Esta prueba submáxima estuvo en concordancia con el método propuesto por Ebbeling et al. (14).
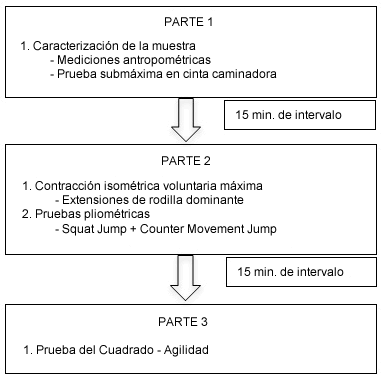
Figura 1. Sesiones de Laboratorio.
Parte 2: Contracción Isométrica Voluntaria Máxima de Cuádriceps y Pruebas Pliométricas
La S isométrica de cuádriceps del sujeto se obtuvo utilizando el aparato de extensión de piernas "Queens" (São Paulo, Brasil) y un dinamómetro portátil "Cefise" (São Paulo, Brasil). Los sujetos se sentaron con 90° de flexión de cadera y 70° de flexión de rodilla, medidos con un goniómetro "Carci" (São Paulo, Brasil), basado en la relación fuerza-longitud (16). El tronco y la parte superior de la pierna dominante se sujetaron a la silla usando cinturones estándar. El brazo inferior del dinamómetro se situó verticalmente de acuerdo con la posición de la rodilla y se fijó con un cinturón que se colocó en la pierna derecha del sujeto. Después de un calentamiento semi-estandarizado con elementos incluidos de estiramiento estático y dinámico, un trote ligero y algunos ejercicios de salto, se realizaron tres contracciones isométricas voluntarias máximas de cuádriceps de 4 segundos cada una con 2 min de descanso entre repeticiones y el mayor valor de F fue tomado para un análisis posterior. El correspondiente torque (T) se determinó usando la ecuación T = F.d.sinθ, donde d es la longitud de la parte inferior de la pierna.
La relación entre S (es decir, F) y m se evaluó usando la técnica alométrica estándar adoptada por Jaric et al. (23). La transformación logarítmica de S = k.mb da log S = log k + b log m una relación lineal entre log S y log m. Por lo tanto, la técnica de regresión lineal aplicada a los datos dio como resultado valores de b correspondientes a F y T para ambos grupos de sujetos probados.
Las pruebas pliométricas se realizaron después del protocolo isométrico. El calentamiento previo a cada prueba, similar al realizado antes de la prueba isométrica voluntaria máxima, se desarrolló con un rango de movimiento articular específico. El rendimiento del salto vertical se midió utilizando una plataforma de fuerza portátil "Cefise" (São Paulo, Brasil). Los sujetos realizaron squat jumps (SJ) y counter movement jumps (CMJ) de acuerdo con los aspectos biomecánicos descritos por Bosco et al. (8). Antes de la prueba, los sujetos realizaron CMJs y SJ submáximos (2 a 3 repeticiones) como práctica y para calentar. Se les pidió que mantuvieran sus manos sobre sus caderas para evitar que los movimientos de los brazos tengan influencia sobre los saltos verticales y para evitar la coordinación como una variable de confusión en la evaluación de los extensores de la pierna (7). Cada sujeto realizó tres SJ y tres CMJ máximos con ~2 min de descanso entre las pruebas. No hubo restricción en el ángulo de flexión de rodilla durante la fase excéntrica e isométrica en el CMJ y se consideró un ángulo inicial (90°) en el SJ (10). Se les pidió que saltaran lo más alto posible y se registró el mejor puntaje (mayor altura - h) y la correspondiente S explosiva (o dinámica), (FSJ y FCMJ). Los valores de FSJ y FCMJ se normalizaron mediante kg1 y kgb (b correspondiente a F y T).
Parte 3: Prueba del Cuadrado – Agilidad
Se utilizó una prueba con cambio de dirección llamada "cuadrado" para medir la agilidad de los corredores voluntarios. Se dibujó un cuadrado en el suelo con cuatro pies de distancia entre los cuatro conos (conos de 0,5 m de altura). El tiempo fue registrado por fotocélulas "Brower Timing System" (Utah, EEUU) situadas en la línea de inicio. Se les pidió a los atletas que corrieran a máxima velocidad y que hicieran sus giros lo más rápido posible. Empezaron con un sprint en dirección diagonal desde la línea de inicio seguido de una carrera hacia un cono en el lado derecho. A continuación, tuvieron que hacer un movimiento diagonal en contra, en la dirección del cono y finalmente correr hacia el último cono posicionado en la marca de inicio. Durante las pruebas, los evaluadores alentaron verbalmente a cada sujeto a lograr el mejor tiempo posible. Cada sujeto tuvo dos intentos con ~3 min de descanso entre las pruebas.
Análisis Estadísticos
Los cálculos estadísticos descriptivos se presentan como medias ± DE. La normalidad de los datos se evaluó mediante la prueba de Shapiro-Wilk. La correlación producto-momento de Pearson se utilizó para investigar las relaciones sin causa-efecto entre la S explosiva (FSJ y FCMJ) y las capacidades físicas (pruebas de rendimiento pliométrico y de agilidad), con y sin la aplicación de exponentes alométricos específicos (relacionados con F y T). Se utilizó un análisis de varianza de medidas repetidas (rANOVA), con la prueba post-hoc de Bonferroni, para evaluar las diferencias estadísticas entre las variables dependientes. Los análisis se realizaron utilizando el programa informático Statistical Package for the Social Sciences (IBM-SPSS, Nueva York, EEUU) versión 20.0, con α = 0,05.
RESULTADOS
En la Tabla 1 se presentan los datos antropométricos y los resultados de la prueba de carrera en cinta caminadora y el rendimiento durante los 5 km. Las relaciones lineales entre S (correspondientes a F y T en la contracción isométrica voluntaria máxima de cuádriceps) y m se presentan en la Figura 2.
Tabla 1. Características Fisiológicas, Resultados de la Prueba de Carrera en Cinta Caminadora y la Prueba de Rendimiento Contrarreloj de 5 km de 24 Corredores Recreativos.
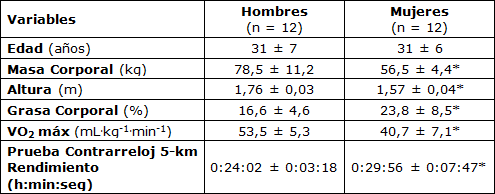
* Diferencias significativas entre hombres y mujeres (P<0,05).
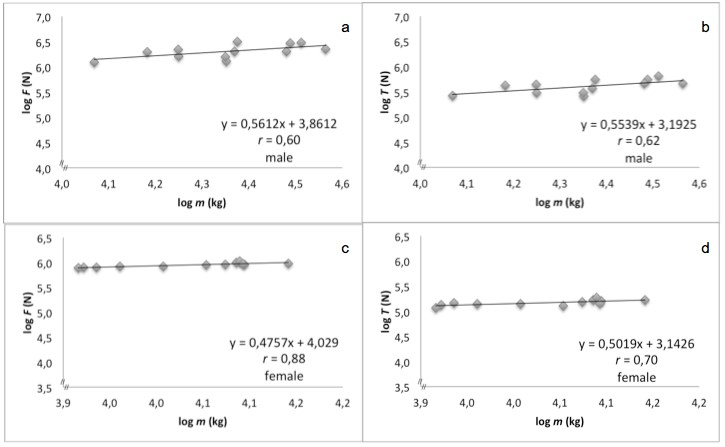
Figura 2. Relaciones Lineales entre S y m de 24 Corredores Recreativos. Exponentes Alométricos correspondientes a F y T (hombre: a - b; mujer: c - d).
Los exponentes alométricos (coeficientes angulares) correspondientes a F y T fueron 0,56 (Figura 2a) y 0,55 (Figura 2b) para el grupo de hombres y 0,48 (Figura 2c) y 0,50 (Figura 2d) para el grupo de mujeres, respectivamente. Los resultados de la prueba pliométrica y de agilidad se presentan en la Tabla 2. Las relaciones entre la S explosiva y las características físicas se presentan en la Tabla 3.
Tabla 2. Pruebas de Rendimiento Pliométrico y de Agilidad de 24 Corredores Recreativos.
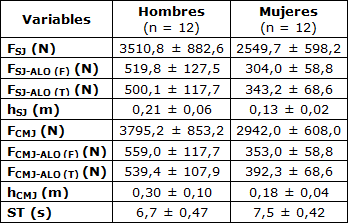
La fuerza explosiva durante el squat jump (SJ) y el counter movement jump (CMJ) sin (FSJ y FCMJ) y con la aplicación de exponentes alométricos específicos (ALO) correspondientes a la fuerza (F) y el torque (T) (FSJ-ALO (F), FCMJ-ALO (F), FSJ-ALO (T) y FCMJ-ALO (T)), pruebas pliométricas (hSJ y hCMJ) y prueba del cuadrado de agilidad (ST).
Tabla 3. Relaciones de S Explosiva con Pruebas de Rendimiento Pliométrico y de Agilidad en 24 Corredores Recreativos.
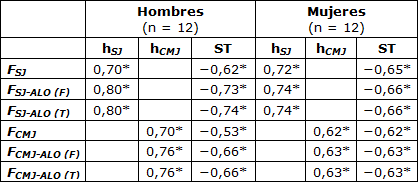
Fuerza explosiva (S) durante el squat jump y el counter movement jump sin (FSJ y FCMJ) y con la aplicación de exponentes alométricos específicos correspondientes a la fuerza (F) y al torque (T) (FSJ-ALO (F), FCMJ-ALO (F), FSJ-ALO (T) y FCMJ-ALO (T)), prueba de rendimiento pliométrico - altura máxima (hSJ y hCMJ) y prueba de rendimiento de agilidad - tiempo (ST). Los resultados se presentaron en valores r con P<0,05 (*).
Se observaron diferencias significativas (P<0,05) entre los grupos de hombres y mujeres en las pruebas de rendimiento pliométrico y de agilidad en todas las variables, lo que indica que el sexo puede tener un impacto directo en las capacidades físicas.
Contrariamente al grupo de mujeres, el grupo de hombres presentó correlaciones más fuertes de S explosiva con las pruebas de rendimiento pliométrico y de agilidad cuando se aplicó la normalización alométrica. Además, el grupo de hombres presentó una mayor variabilidad de m (14,2%) en comparación con el grupo de mujeres (7,7%) (ver Tabla 1), con valores de densidad corporal de 1,061 y 1,045 g.ml-1, respectivamente. Estos aspectos morfológicos son exponentes alométricos específicos (40).
DISCUSIÓN
El objetivo del presente estudio fue examinar las relaciones alométricas entre la S explosiva de los miembros inferiores y las pruebas de capacidad física. La hipótesis que sustenta este estudio fue que se puede emplear un método de escala alométrica para ajustar la S al tamaño corporal y predecir las capacidades físicas en corredores recreativos. Los principales hallazgos fueron: (a) la S explosiva de los miembros inferiores es un predictor de las pruebas de pliometría y de agilidad; y (b) el modelo de escala alométrica se puede usar para ajustar la S al tamaño corporal y predecir las capacidades físicas en corredores recreativos que son morfológicamente diferentes.
Las pruebas de fuerza se usan comúnmente para valorar, evaluar y comparar datos relacionados con la función muscular en entornos atléticos, clínicos y de rehabilitación. La capacidad de comparar la S entre y dentro de los grupos también es importante en la investigación. Los resultados de las pruebas de fuerza se confunden con frecuencia por el tamaño corporal y pueden surgir incoherencias cuando los datos de fuerza no se normalizan para el tamaño corporal o se normalizan usando métodos inapropiados (22). Los métodos absolutos de pruebas de fuerza tienden a producir un sesgo hacia individuos más grandes (41), mientras que los métodos de ratio (es decir, S relativa a m) tienden a producir un sesgo hacia individuos más pequeños (3). La normalización de la S en relación con el área de sección transversal del músculo se ha propuesto como el gold standard (25). Sin embargo, recientemente demostramos que el área de sección transversal del músculo no produjo la relación esperada con la S isométrica en una gran cohorte de hombres adultos (44). Se han propuesto modelos de escala alométrica, por lo general con masa libre de grasa, como un enfoque alternativo para controlar las diferencias en el tamaño corporal y/o la masa muscular (9,23).
El exceso de adiposidad, como en individuos con sobrepeso u obesidad, representa una posible confusión para la escala alométrica cuando se usa m o incluso el área de sección transversal del músculo como variables de escala, especialmente en las mujeres. Lafortuna et al. (27) y Sartorio et al. (37) encontraron que una mayor m en los hombres fue debido a "contribuciones similares de masa libre de grasa y grasa, pero principalmente contribuido por masa grasa en las mujeres". Ambos estudios mostraron que el índice de m (IMC) se asoció significativa y positivamente con la fuerza muscular en los hombres. Sin embargo, en las mujeres, Lafortuna et al. (27) encontraron que el IMC no tiene asociación con la fuerza muscular, mientras que Sartorio et al. (37) encontraron una asociación significativa pero muy débil. Estos datos sugieren que la escala alométrica de la fuerza muscular usando m como la variable de escala puede ser confundida por la contribución relativa de la masa grasa, especialmente en las mujeres (45). Estos hallazgos y la variabilidad de m podrían explicar nuestros resultados, justificando un mejor efecto de la estandarización alométrica en el grupo de hombres (ver Tabla 3).
Varios estudios recientes han utilizado diferentes enfoques para evaluar el parámetro exponencial b que proporciona resultados independientes de m cuando la S registrada se dividió por mb. Por ejemplo, se obtuvo b = 0,51 para la F de agarre (41), mientras que se obtuvo b = 0,45 – 0,48 para la F ejercida contra una carga externa (4). Cuando se probó el T máximo de diferentes grupos musculares, los valores evaluados obtenidos fueron más altos: b = 1 (42), b = 0,74 (12) y b = 0,91 – 1,10 (29). Contrariamente, nuestros resultados mostraron valores similares de F en comparación con T (es decir, b = 0,56 y 0,55 para el hombre; 0,48 y 0,50 para la mujer, respectivamente), que contradicen los hallazgos de los estudios antes mencionados. Un posible factor confuso en los valores de b podría deberse a la relación entre m y el tamaño corporal, que está determinada por el principio llamado similitud geométrica o biológica (30).
Tanto el SJ como el CMJ se usan comúnmente para medir la capacidad de salto de los atletas. El SJ se usa como un indicador de la fuerza concéntrica de los miembros inferiores, mientras que el CMJ se emplea como un indicador de la fuerza reactiva de los miembros inferiores (33). Al usar las dos variaciones de la prueba de salto, también es posible calcular la influencia del ciclo de estiramiento-acortamiento, que se ha identificado como un factor físico fundamental en una variedad de deportes (28). Por ejemplo, Komi y Bosco (26) informaron diferencias generales en la altura saltada por mujeres del 54 al 67% por debajo de la alcanzada por hombres al realizar un SJ y un CMJ, y esto se atribuyó a que las mujeres tenían una masa muscular reducida de las extremidades inferiores. En nuestro estudio, las diferencias fueron del 23 y 27% (kg1) y del 37 y 42% aproximadamente (kgb).
Estudios previos han demostrado claramente que el movimiento de resorte de los músculos del miembro inferior (por ejemplo, saltar y correr) se ve afectado por la rigidez total activa y pasiva del sistema musculoesquelético, incluidos los músculos, tendones y ligamentos (15,17). Bojsen-Moller et al. (6), observaron una correlación entre la S explosiva y las pruebas de rendimiento pliométrico (en SJ y CMJ) en atletas de alto nivel, lo que sugiere que la producción de S explosiva está relacionada positivamente con la rigidez de las estructuras de los órganos del tendón, posiblemente a través de una transmisión más eficiente de la S de los elementos contráctiles a los huesos. Algunos autores sugieren que una mayor masa muscular indica una mayor cantidad de tejido conectivo, lo que implica un mayor número de fibras de colágeno posicionadas paralelamente, lo que también influye en la resistencia a la deformación del músculo (18). Por lo tanto, la cantidad de tejido contráctil y conectivo presente en el músculo parece ser crucial para la rigidez pasiva, lo que posiblemente limita la contribución de la flexibilidad a la medida de rigidez y justifica el uso de una estandarización particular de la S explosiva (por ej., modelo de escala alométrica) para predecir las capacidades físicas de los corredores recreativos como se observó en nuestro estudio. Probablemente, la expresión alométrica de fuerza y/o torque podría explicar mejor los hallazgos previos relacionados con los efectos de las intervenciones de entrenamiento de fuerza máxima/explosiva en la economía y el rendimiento en corredores recreativos (5,19,34,35,39).
CONCLUSIONES
Se considera que las capacidades de fuerza son un factor importante que afecta el rendimiento de los corredores recreativos de media distancia. Según numerosos autores, el desarrollo de estas capacidades debería ser una prioridad para los corredores recreativos ya que la S es un componente importante de la resistencia. Su importancia aumenta considerablemente junto con la mejora de las habilidades deportivas de los corredores. Se han propuesto o aplicado diferentes métodos de ajuste de S para normalizar las diferencias en diversas estimaciones del tamaño corporal, como m, cuando se presentan los resultados de las pruebas de función muscular en diversos estudios médicos, ergonómicos y relacionados con el deporte. Un ejemplo es la escala alométrica, un método no estándar que se puede emplear para ajustar la S al tamaño corporal y proporcionar información adicional de alguna manera, ya sea sobre la fisiología subyacente o para fines de predicción del rendimiento.
AGRADECIMIENTOS:
Fundación Araucária / PR, Brasil
Dirección de correo: Marcus P. Tartaruga, PhD, Midwest State University of Paraná, Guarapuava, Paraná, Brazil. Email: mtartaruga@unicentro.br or mtartaruga@hotmail .com
Referencias
1. Alemdaroglu U. (2012). The relationship between muscle strength, anaerobic performance, agility, sprint ability and vertical jump performance in professional basketball players. J Hum Kinet. 2012;31:149-158.
2. Alexander MJ. (1989). The relationship between muscle strength and sprint kinematics in elite sprinters. Can J Sport Sci. 1989;14:148-157.
3. Atkins SJ. (2004). Normalizing expressions of strength in elite rugby league players. J Strength Cond Res. 2004;18:53-58.
4. Batterham AM, George KP. (1997). Allometric modeling does not determine a dimensionless power function ratio for maximal muscular function. J Appl Physiol. 1997;83:2158-2166.
5. Beattie K, Kenny IC, Lyons M, Carson BP. (2014). The effect of strength training on performance in endurance athletes. Sports Med. 2014;44:845-865.
6. Bojsen-Moller J, Magnusson SP, Rasmussen LR, et al. (2005). Muscle performance during maximal isometric and dynamic contractions is influenced by the stiffness of the tendinous structures. J Appl Physiol (1985). 2005;99:986-994.
7. Bosco C, Belli A, Astrua M, et al. (1995). A dynamometer for evaluation of dynamic muscle work. Eur J Appl Physiol Occup Physiol. 1995;70:379-386.
8. Bosco C, Luhtanen P, Komi PV. (1983). A simple method for measurement of mechanical power in jumping. Eur J Appl Physiol Occup Physiol. 1983;50:273-282.
9. Comfort P, Pearson SJ. (2014). Scaling--which methods best predict performance? J Strength Cond Res. 2014;28:1565-1572.
10. Correa CS, Laroche DP, Cadore EL, et al. (2012). Different types of strength training in older women. Intern J Sports Med. 2012;33:1-8.
11. Cronin JB, Hansen KT. (2005). Strength and power predictors of sports speed. J Strength Cond Res. 2005;19:349-357.
12. Davies MJ, Dalsky GP. (1997). Normalizing strength for body size differences in older adults. Med Sci Sports Exerc. 1997;29:713-717.
13. Dowson MN, Nevill ME, Lakomy HK, et al. (1998). Modelling the relationship between isokinetic muscle strength and sprint running performance. J Sports Sci. 1998;16:257 -265.
14. Ebbeling CB, Ward A, Puleo EM, et al. (1991). Development of a single-stage submaximal treadmill walking test. Med Sci Sports Exerc. 1991;23(8):966-973.
15. Farley CT, Ferris DP. (1998). Biomechanics of walking and running: Center of mass movements to muscle action. Exerc Sport Sci Rev. 1998;26:253-285.
16. Fenn WO, Marsh BS. (1935). Muscular force at different speeds of shortening. J Physiol. 1935;85:277-297.
17. Ferris DP, Louie M, Farley CT. (1998). Running in the real world: Adjusting leg stiffness for different surfaces. Proc Biol Sci. 1998;265:989-994.
18. Gajdosik RL. (2001). Passive extensibility of skeletal muscle: Review of the literature with clinical implications. Clin Biomech (Bristol, Avon). 2001;16:87-101.
19. Guglielmo LG, Greco CC, Denadai BS. (2009). Effects of strength training on running economy. Int J Sports Med. 2009;30:27-32.
20. Iossifidou A, Baltzopoulos V, Giakas G. (2005). Isokinetic knee extension and vertical jumping: Are they related? J Sports Sci. 2005;23:1121-1127.
21. Jackson AS, Pollock ML. (1978). Generalized equations for predicting body density of men. Br J Nutr. 1978;40:497-504.
22. Jaric S, Mirkov D, Markovic G. (2005). Normalizing physical performance tests for body size: A proposal for standardization. J Strength Cond Res. 2005;19:467-474.
23. Jaric S, Radosavljevic-Jaric S, Johansson H. (2002). Muscle force and muscle torque in humans require different methods when adjusting for differences in body size. Eur J Appl Physiol. 2002;87:304-307.
24. Kispert CP, Merrifield HH. (1987). Interrater reliability of skinfold fat measurements. Phys Ther. 1987;67:917-920.
25. Klein CS, Rice CL, Marsh GD. (2001). Normalized force, activation, and coactivation in the arm muscles of young and old men. J Appl Physiol (1985). 2001;91:1341-1349.
26. Komi PV, Bosco C. (1978). Utilization of stored elastic energy in leg extensor muscles by men and women. Med Sci Sports. 1978;10:261-265.
27. Lafortuna CL, Agosti F, Marinone PG, et al. (2004). The relationship between body composition and muscle power output in men and women with obesity. J Endocrinol Invest. 2004;27:854-861.
28. McGuigan MR, Doyle TL, Newton M, et al. (2006). Eccentric utilization ratio: Effect of sport and phase of training. J Strength Cond Res. 2006;20:992-995.
29. Neder JA, Nery LE, Silva AC, et al. (1999). Maximal aerobic power and leg muscle mass and strength related to age in non-athlethic males and females. Eur J Appl Physiol Occup Physiol. 1999;79:522-530.
30. Nevill AM, Stewart AD, Olds T, Holder R. (2004). Are adult physiques geometrically similar? The dangers of allometric scaling using body mass power laws. Am J Phys Anthropol. 2004;124:177-182.
31. Nevill AM, Winter EM, Ingham S, Watts A, et al. (2010). Adjusting athletes' body mass index to better reflect adiposity in epidemiological research. J Sports Sci. 2010;28:1009-1016.
32. Newman MA, Tarpenning KM, Marino FE. (2004). Relationships between isokinetic knee strength, single-sprint performance, and repeated-sprint ability in football players. J Strength Cond Res. 2004;18:867-872.
33. Newton RU, Kraemer WJ, Hakkinen K. (1999). Effects of ballistic training on preseason preparation of elite volleyball players. Med Sci Sports Exerc. 1999;31:323-330.
34. Paavolainen L, Hakkinen K, Hamalainen I, Nummela A, Rusko H. (1999). Explosive-strength training improves 5-km running time by improving running economy and muscle power. J Appl Physiol. 1999;86:1527-1533.
35. Ramirez-Campillo R, Alvarez C, Henriquez-Olguin C, et al. (2014). Effects of plyometric training on endurance and explosive strength performance in competitive middle- and long-distance runners. J Strength Cond Res. 2014;28:97-104.
36. Rubner M. (1883). Concerning the influence of body size on energy metabolism. Z Biol. 1883; 19:536-562.
37. Sartorio A, Proietti M, Marinone PG, Agosti F, et al. (2004). Influence of gender, age and BMI on lower limb muscular power output in a large population of obese men and women. Int J Obes Relat Metab Disord. 2004;28:91-98.
38. Siri WE. (1993). Body composition from fluid spaces and density: Analysis of methods. 1961. Nutrition. 1993;9:480-491.
39. Storen O, Helgerud J, Stoa EM, Hoff J. (2008). Maximal strength training improves running economy in distance runners. Med Sci Sports Exerc. 2008;40:1087-1092.
40. Tartaruga MP, Mota CB, Peyre Tartaruga LA, et al. (2013). Running efficiency and long-distance performance prediction: Influence of allometric scaling. Sci Sports. 2013; 28:165-171.
41. Vanderburgh PM, Mahar MT, Chou CH. (1995). Allometric scaling of grip strength by body mass in college-age men and women. Res Q Exerc Sport. 1995;66:80-84.
42. Weir JP, Housh TJ, Johnson GO, Housh DJ, Ebersole KT. (1999). Allometric scaling of isokinetic peak torque: The Nebraska Wrestling Study. Eur J Appl Physiol Occup Physiol. 1999;80:240-248.
43. West GB, Brown JH, Enquist BJ. (1997). A general model for the origin of allometric scaling laws in biology. Science. 1997;276:122-126.
44. Zoeller RF, Ryan ED, Gordish-Dressman H, Price TB, Seip RL, et al. (2007). Allometric scaling of biceps strength before and after resistance training in men. Med Sci Sports Exerc. 2007;39:1013-1019.
45. Zoeller RF, Ryan ED, Gordish-Dressman H, et al. (2008). Allometric scaling of isometric biceps strength in adult females and the effect of body mass index. Eur J Appl Physiol. 2008;104:701-710.
Cita Original
Batista MM, Lopes KA, Queiroga MR, Peyré-Tartaruga LA, Tartaruga MP. Las Relaciones Alométricas entre la Fuerza Explosiva de los Miembros Inferiores y el Rendimiento en las Pruebas de Capacidades Físicas. JEPonline 2018;21(3):171-182.
Cita en PubliCE
Mayara M. Batista, Karina A. Lopes, Marcos R. Queiroga, Leonardo A. Peyré-Tartaruga Marcus P. Tartaruga (2018). Las Relaciones Alométricas entre la Fuerza Explosiva de los Miembros Inferiores y el Rendimiento en las Pruebas de Capacidades Físicas. .https://g-se.com/las-relaciones-alometricas-entre-la-fuerza-explosiva-de-los-miembros-inferiores-y-el-rendimiento-en-las-pruebas-de-capacidades-fisicas-2457-sa-o5b7c3930e37a2
