Evaluación del Perfil Carga-Velocidad en el Ejercicio Prone Bench Pull con Peso Libre mediante Diferentes Variables de Velocidad y Modelos de Regresión

Resumen

Los objetivos de este estudio fueron (I) determinar la variable de velocidad y el modelo de regresión que mejor se ajustaban a la relación carga-velocidad durante el ejercicio prone bench pull con peso libre, (II) comparar la fiabilidad de la velocidad alcanzada en cada porcentaje de una repeticicón máxima (1RM) entre diferentes variables de velocidad y modelos de regresión, y (III) comparar la variabilidad intra- y entre-sujetos de la velocidad alcanzada en cada %1RM. Dieciocho hombres (14 remeros y 4 levantadores de pesas) realizaron un test incremental durante el ejercicio prone bench pull con peso libre en dos sesiones diferentes. Las relaciones carga-velocidad generales e individuales se modelaron a través de tres variables de velocidad (velocidad media [MV], velocidad media propulsiva [MPV] y velocidad máxima [PV]) y dos modelos de regresión (lineal y polinomial de segundo grado). Los principales hallazgos revelaron que (I) las relaciones carga-velocidad generales (rango del coeficiente de correlación [r] de Pearson = 0,964-0,973) e individuales (mediana r = 0,986 para MV, 0,989 para MPV, y 0,984 para PV) eran altamente lineales, (II) la fiabilidad de la velocidad alcanzada en cada %1RM no difería significativamente entre las variables de velocidad (rango del coeficiente de variación [CV] = 2,55-7,61% para MV, 2,84-7,72% para MPV y 3,50-6,03% para PV) ni entre los modelos de regresión (rango de CV = 2,55-7,72% y 2,73-5,25% para las regresiones lineal y polinomial, respectivamente), y (III) la variabilidad intra-sujetos de la velocidad alcanzada en cada %1RM fue menor que la variabilidad entre-sujetos para las cargas ligeras-moderadas. No se observaron diferencias significativas entre los CVs intra-sujeto y entre-sujetos para la MV del test de 1RM (6,02% versus 6,60%; CVratio = 1,10), mientras que el CV intra-sujeto fue menor para la PV (6,36% versus 7,56%; CVratio = 1,19). Estos resultados sugieren que la relación carga-MV individual debe determinarse con un modelo de regresión lineal para obtener la prescripción más precisa de la carga relativa durante el ejercicio prone bench pull con peso libre.

Versión PDF

INTRODUCCIÓN

El uso de la tecnología en el deporte puede proporcionar información para optimizar la prescripción y el seguimiento de los programas de entrenamiento [1,2]. Además, la mejora de la asequibilidad y disponibilidad de la tecnología ha permitido el desarrollo de nuevas metodologías de entrenamiento como el "entrenamiento de la fuerza basado en la velocidad" [3-5]. El entrenamiento de la fuerza basado en la velocidad requiere la medición de la velocidad en tiempo real y proporciona al menos tres aplicaciones prácticas importantes: (I) la carga puede ajustarse diariamente para que coincida con la intensidad deseada (comúnmente expresada como porcentaje de una repetición máxima; 1RM) debido a la fuerte relación entre la velocidad de movimiento y la carga levantada [6,7], (II) el volumen de la sesión de entrenamiento (por ejemplo, el número de ejercicios por sesión, series por ejercicio o repeticiones por serie) puede prescribirse en función de la magnitud de la pérdida de velocidad debido a su estrecha relación con los marcadores de fatiga [8,9], y (III) la administración del feed-back de velocidad en tiempo real mejora la motivación y permite el mantenimiento de velocidades de movimiento más altas durante el entrenamiento de la fuerza, lo que a su vez puede estimular las adaptaciones del entrenamiento a largo plazo [10,11]. A pesar de estas aplicaciones alentadoras, muchos aspectos relacionados con el enfoque del entrenamiento de la fuerza basado en la velocidad aún necesitan ser investigados para facilitar y optimizar la aplicación de esta novedosa metodología de entrenamiento de la fuerza.

Una de las aplicaciones más comúnmente investigadas del entrenamiento de la fuerza basado en la velocidad es la posibilidad de utilizar la velocidad de movimiento para determinar qué %1RM se está levantando [6,7,12-15]. Las ecuaciones generales de relación carga-velocidad que permiten estimar el %1RM basado en la velocidad registrada con una carga submáxima se propusieron originalmente para el ejercicio de press de banca [6]. Esto se ha completado a través de una serie de ejercicios de entrenamiento de la fuerza tales como sentadilla, salto vertical, press de banca y bech pull [7,12-15]. Dos de las consideraciones metodológicas más importantes a la hora de proponer ecuaciones de relación carga-velocidad son: la variable de velocidad (por ejemplo, la velocidad media [MV], la velocidad media propulsiva [MPV] o la velocidad máxima [PV]) y el modelo de regresión (por ejemplo, los polinomiales de primer o segundo grado) [12,16]. Estudios previos han sugerido que la modelización de la MV a través de una regresión lineal debería utilizarse para maximizar la precisión de la relación carga-velocidad durante el ejercicio de press de banca [12,16]. Sin embargo, debido a los patrones de movimiento únicos de cada ejercicio, es importante explorar si los hallazgos anteriores obtenidos con el ejercicio de press de banca podrían extenderse a otro ejercicio comúnmente usado en el tren superior del cuerpo, como el prone bench pull.

Se han realizado dos estudios para explorar la relación carga-velocidad general durante el ejercicio prone bench pull [14,17]. Sánchez-Medina et al. [14] examinaron la relación carga-velocidad durante el ejercicio bench pull, realizado en una máquina Smith, a través de un modelo de regresión polinomial utilizando las variables MV y MPV. Además, Loturco et al. [17] modelaron la relación carga-velocidad durante el ejercicio prone bench pull con peso libre a través de un modelo de regresión lineal usando MV, MPV y PV. Tanto Sánchez-Medina et al. [14] (r2= 0,95-0,96 y error estándar de estimación [SEE] = 5,31-5,90%1RM) como Loturco et al. [17] (r2 = 0,90-0,91 y SEE = 6,27-6,56%1RM) recomendaron el uso de sus ecuaciones generales de relación carga-velocidad para estimar el %1RM. Sin embargo, ningún estudio previo ha comparado directamente qué modelo de regresión (lineal o polinomial de segundo grado) proporciona el método más preciso para determinar la relación carga-velocidad durante el ejercicio bench pull. Además, la fiabilidad entre-sesiones de la relación carga-velocidad (es decir, la velocidad alcanzada en cada %1RM) nunca ha sido evaluada durante el ejercicio bench pull. La relación carga-velocidad debe determinarse en dos días diferentes para calcular la variabilidad intra-sujeto de la velocidad alcanzada en cada %1RM. Nótese que Sánchez-Medina et al. [14] y Loturco et al. [17] sólo examinaron la variabilidad entre-sujetos, ya que sus sujetos sólo fueron probados una vez. Por lo tanto, creemos que determinar la precisión y fiabilidad de ambos modelos de regresión (lineal y polinomial) para obtener la relación carga-velocidad durante el ejercicio bench pull presenta un interés práctico.

Para abordar las lagunas existentes en la bibliografía, es necesario examinar más a fondo la relación carga-velocidad durante el ejercicio prone bench pull con peso libre. Por lo tanto, los objetivos de este estudio fueron (I) determinar el modelo de regresión (lineal versus polinomial de segundo grado) que es capaz de ajustar mejor la relación carga-velocidad considerando las diferentes variables de velocidad (MV, MPV y PV), (II) comparar la fiabilidad de la velocidad alcanzada en cada %1RM entre diferentes variables de velocidad y modelos de regresión, y (III) comparar la variabilidad intra- y entre-sujetos de la velocidad alcanzada en cada %1RM. Generamos la hipótesis de que (I) las relaciones carga-velocidad generales e individuales serían altamente lineales independientemente de la variable de velocidad considerada [14,17], (II) la PV y el modelo de regresión lineal proporcionarían la menor variabilidad intra-sujeto de la velocidad alcanzada en cada %1RM [12,16], y (III) la variabilidad intra-sujeto de la velocidad alcanzada en cada %1RM sería menor que la variabilidad entre-sujetos [16].

MATERIALES Y MÉTODOS

Sujetos

Dieciocho hombres (14 remeros y cuatro levantadores de pesas) participaron en este estudio (media ± desviación estándar [SD]: edad = 20,6 ± 2,7 años [rango: 16-25 años]; masa corporal = 72,5 ± 9,1 kg; altura = 1,74 ± 0,07 m; 1RM de prone bench pull = 89,9 ± 12,6 kg; experiencia de entrenamiento en prone bench pull= 6,2 ± 4,2 años). A los sujetos no se les permitió realizar ningún ejercicio extenuante durante las 24 horas previas a cada sesión de prueba. Ninguno de los sujetos tenía lesiones o dolor musculoesquelético que pudieran comprometer los resultados del presente estudio. Antes de la prueba, los sujetos fueron informados sobre el propósito y los procedimientos de la investigación, y ellos o sus tutores legales (para los sujetos de < 18 años) dieron su consentimiento por escrito para participar en el estudio. El experimento fue aprobado por el Comité de Ética local de la Universidad de Granada (491/CEIH/2018) según la Declaración de Helsinki.

Diseño Experimental

Se utilizó un diseño de medidas repetidas para investigar diferentes aspectos metodológicos relacionados con la evaluación del perfil carga-velocidad durante el ejercicio prone bench pull con peso libre. Los sujetos realizaron un test de carga incremental desde 20 kg hasta la carga de 1RM, durante dos sesiones separadas por 72-96 horas. Las relaciones carga-velocidad generales e individuales se modelaron a través de tres variables de velocidad diferentes (MV, MPV y PV) y dos modelos de regresión (lineal y polinomial de segundo grado). Todas las sesiones de prueba se realizaron entre las 15:00 y las 19:00 horas.

Procedimientos de Prueba

Cada sesión de prueba comenzó con un calentamiento estandarizado que consistía en 5 minutos de trote, seguido de ejercicios de movilidad articular, y una serie de cinco repeticiones realizadas con una carga externa de 20 kg (es decir, la masa de la barra olímpica utilizada durante el test) durante el ejercicio prone bench pull con peso libre. La carga externa inicial de test de carga incremental fue de 20 kg para todos los sujetos y fue aumentando progresivamente en 10 kg hasta que la MV fue inferior a 0,80 m·s-1 (≈ 70%1RM). Después, la carga se incrementó en pasos de 5 a 1 kg hasta que se alcanzó la carga de 1RM. Se realizaron tres repeticiones con cargas ligeras (MV > 1,10 m·s-1), dos con cargas medias (1,10 m·s-1 ≤ MV ≤ 0,80 m·s-1) y una con cargas pesadas (MV < 0,80 m·s-1). El reposo intra-serie entre las repeticiones fue de 10 segundos y el reposo inter-serie fue de 5 minutos. Los sujetos recibieron feedback de velocidad inmediatamente después de cada repetición y se les animó a realizar todas las repeticiones a la máxima velocidad prevista.

El ejercicio bench pull se realizó con una barra olímpica estándar y discos de pesas calibrados (Eleiko, Halmstad, Suecia). La posición inicial implicaba a los sujetos acostados en decúbito prono, el mentón en contacto con el banco, los codos completamente extendidos y un agarre prono de la barra ligeramente más ancho que el ancho de hombros. Desde esa posición, se les instruyó a los sujetos que traccionen de la barra lo más rápido posible hasta que entrara en contacto con la parte inferior del banco. Una repetición no se consideraba válida si la barra no contactaba con la parte inferior del banco. Las piernas se sostuvieron durante todas las repeticiones por un investigador y el mentón permaneció en contacto con el banco en todo momento. El grosor del banco era de 8,5 cm.

Equipamiento de Medición y Análisis de Datos

Un transductor de velocidad lineal (T-Force System; Ergotech, Murcia, España) se colocó en el lado derecho de la barra y registró la velocidad vertical a una frecuencia de 1.000 Hz. En el presente estudio se consideraron tres variables de velocidad: Valor de la velocidad media-MV desde el inicio de la fase concéntrica hasta que la velocidad de la barra sea 0 m·s-1; valor de la velocidad media-MPV desde el inicio de la fase concéntrica hasta que la aceleración de la barra sea inferior a la gravedad (-9,81 m·s-2); valor de la velocidad instantánea máxima-PV alcanzada durante la fase concéntrica [12]. Para el análisis posterior sólo se utilizó la repetición con el valor de velocidad más alto (MV, MPV o PV como criterio para sus respectivas relaciones carga-velocidad) de cada condición de carga.

Las repeticiones de todos los sujetos se agruparon para determinar las relaciones generales carga-velocidad (se proporcionaron 6 ecuaciones: 3 variables × 2 modelos de regresión). También se determinaron las relaciones de carga-velocidad individual y se representaron las velocidades alcanzadas en cada %1RM (en incrementos del 5% desde 20%1RM hasta 100%1RM). Las relaciones carga-velocidad generales e individuales se modelaron aplicando polinomios de primer y segundo grado a los datos [16]. Los datos de la primera sesión de prueba se utilizaron para explorar las relaciones generales de carga-velocidad, mientras que los datos de ambas sesiones de prueba se utilizaron para analizar las relaciones individuales de carga-velocidad.

Análisis Estadísticos

Los datos descriptivos se presentan como medias y SD, mientras que el coeficiente de correlación de Pearson (r) se presenta a través de sus valores medios y rango. La relación entre la carga relativa (%1RM) y las tres variables de velocidad (MV, MPV y PV) se evaluó mediante modelos de regresión lineal y polinomial de segundo grado. La bondad de ajuste de las relaciones carga-velocidad general e individual se evaluó mediante el coeficiente r y la estadística F. La linealidad de las relaciones carga-velocidad individuales también se comparó entre las tres variables de velocidad a través de un ANOVA de medidas repetidas unidireccional aplicado a los coeficientes r. El error estándar de la medición (SD intra-sujeto), el coeficiente de variación (CV (%) = ) y el coeficiente de correlación intraclase (ICC, modelo 3.1) se utilizaron para explorar la fiabilidad de los valores de velocidad alcanzados en cada %1RM obtenidos a partir de las relaciones carga-velocidad individuales, así como la velocidad del test de 1RM. La fiabilidad aceptable se determinó como un CV < 10% [18]. La relación entre dos CVs se utilizó para comparar la fiabilidad entre las diferentes variables de velocidad y los modelos de regresión. La relación de CV también se utilizó para comparar el CV intra-sujeto de los valores de velocidad alcanzados en cada %1RM con el CV entre-sujetos (CV (%) = ). El valor de 1,15 se consideró como la relación CV más pequeña e importante [19]. El análisis de fiabilidad se realizó mediante una hoja de cálculo personalizada [20], mientras que el SPSS (versión 22.0; SPSS, Inc., Chicago, IL) se utilizó para otros análisis estadísticos. Alfa se fijó en 0,05.

RESULTADOS

Las relaciones generales de carga-velocidad fueron fuertes para las tres variables de velocidad (r ≥ 0,93; Fig 1). El modelo de regresión lineal proporcionó una estadística F más alta en comparación con el modelo de regresión polinomial para la MV y la MPV, mientras que no se observaron diferencias significativas en la magnitud de la estadística F entre ambos modelos de regresión para la PV. Las relaciones carga-velocidad individuales también fueron altamente lineales para las tres variables de velocidad (r mediana [rango] = 0,986 [0,945, 0,999] para la MV, 0,989 [0,939, 0,998] para la MPV, y 0,984 [0,967, 0,997] para la PV). La linealidad de las relaciones carga-velocidad individuales no difirió significativamente entre las tres variables de velocidad (F = 1,26; p = 0,296). La SD promedio y entre-sujetos de los valores de velocidad asociados con cada %1RM se muestran en la Tabla 1.

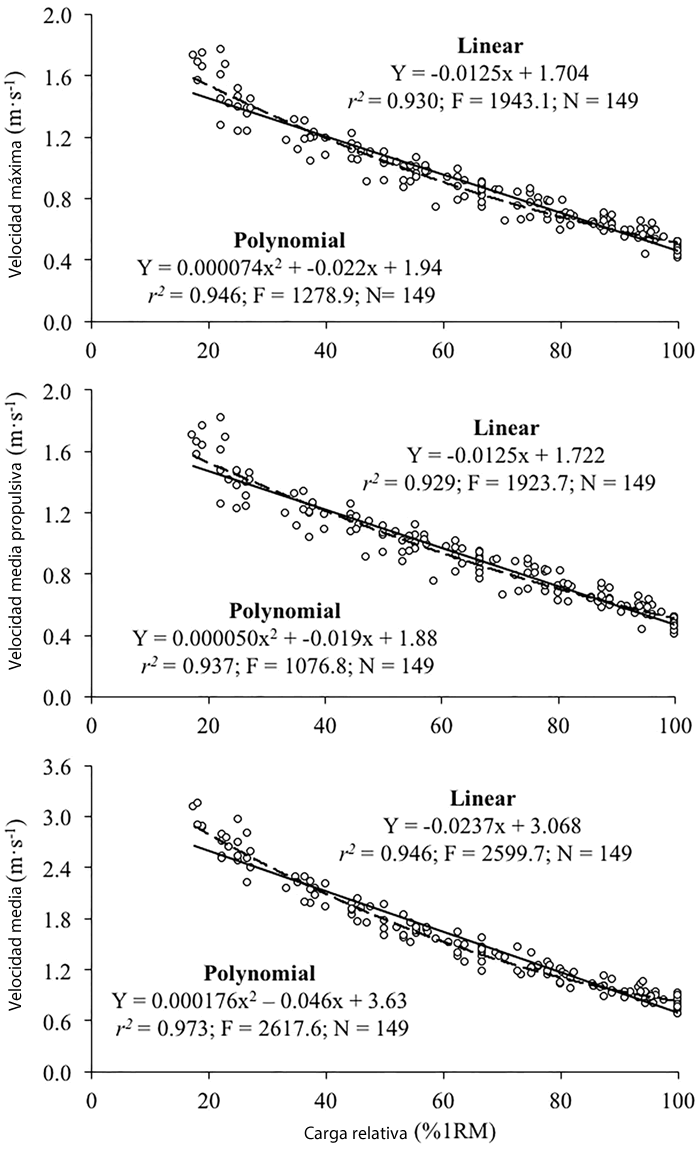
Figura 1. Generalizada a través de la relación de los sujetos entre la carga relativa (%1RM) y la velocidad media (panel superior), la velocidad media propulsiva (panel medio) y la velocidad máxima (panel inferior) en el ejercicio bench pull.

Se representan las ecuaciones de regresión lineal (línea sólida) y polinomial de segundo grado (línea discontinua). r2, coeficiente de determinación de Pearson; F, estadística F; N = número de ensayos incluidos en el análisis de regresión.
https://doi.org/10.1371/journal.pone.0212085.g001

Tabla 1. Valores de velocidad asociados a cada carga relativa (%1RM) obtenidos a partir de las relaciones carga-velocidad individuales modeladas mediante modelos de regresión lineal y polinomial de segundo grado.
https://doi.org/10.1371/journal.pone.0212085.t001

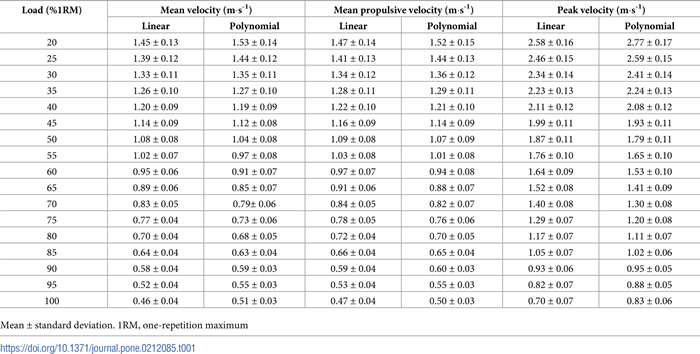
Se observó una fiabilidad aceptable (CV < 10%) en todas las cargas relativas para las tres variables de velocidad y los dos modelos de regresión (Tabla 2). También se observó un valor de ICC significativo en todas las cargas relativas, a excepción de las cargas pesadas (85-100%1RM) para la MV y la MPV y las cargas moderadas (45-60%1RM) para la PV modelada mediante un modelo de regresión polinomial (Tabla 3). La fiabilidad de las relaciones completas carga-velocidad no difirió significativamente entre las variables de velocidad o entre los modelos de regresión. Sin embargo, la MV generalmente proporcionaba la mayor fiabilidad con las cargas ligeras y la PV era la variable más fiable con cargas más elevadas. El modelo de regresión lineal generalmente proporcionó una mayor fiabilidad (menor CV y mayor ICC) a cargas relativas ligeras-moderadas (20-80%1RM), mientras que el modelo de regresión polinomial proporcionó una mayor confiabilidad con las cargas relativas pesadas (90-100%1RM).

Tabla 2. Coeficiente de variación (CV) intra-sujeto con intervalos de confianza del 95% obtenidos en cada carga relativa para cada variable de velocidad y modelo de regresión.
https://doi.org/10.1371/journal.pone.0212085.t002

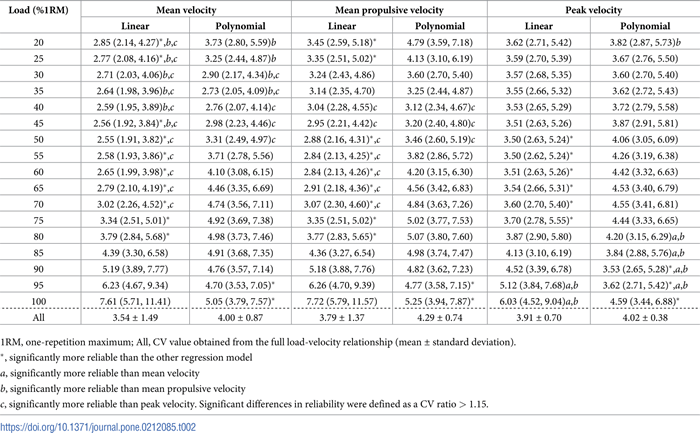
Tabla 3. Coeficiente de correlación intraclase (ICC) con intervalos de confianza del 95% obtenidos en cada carga relativa para cada variable de velocidad y modelo de regresión.
https://doi.org/10.1371/journal.pone.0212085.t003

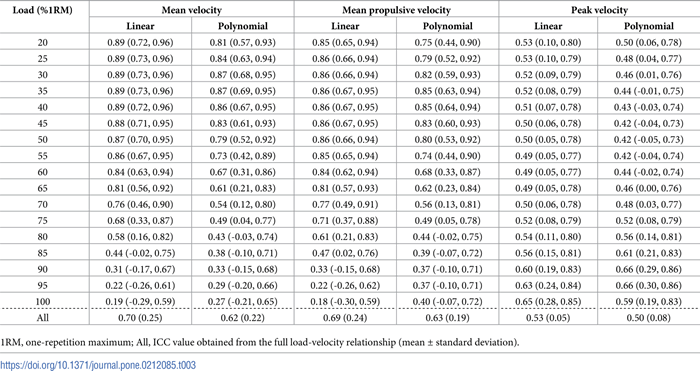
El CV intra-sujeto de los valores de velocidad asociados con cada %1RM fue generalmente más bajo que el CV entre-sujetos (Fig. 2). La magnitud de las diferencias entre el CV intra-sujeto y entre-sujetos fue consistente a través de las cargas para la PV, mientras que las diferencias tendieron a disminuir con el incremento de la carga para la MV y la MPV. Los valores de MV y PV del test de 1RM fueron 0,479 ± 0,032 m·s-1 y 0,790 ± 0,060 m·s-1, respectivamente. No se observaron diferencias significativas entre los CVs intra-sujeto y entre-sujetos para la MV del test de 1RM (6,02% versus 6,60%; ratio de CV = 1,10), mientras que el CV intra-sujeto fue menor para la PV (6,36% versus 7,56%; ratio de CV = 1,19). Se observó un bajo ICC en el caso de la MV y la PV registradas durante el test de 1RM (ICC = 0,18 y 0,31, respectivamente).

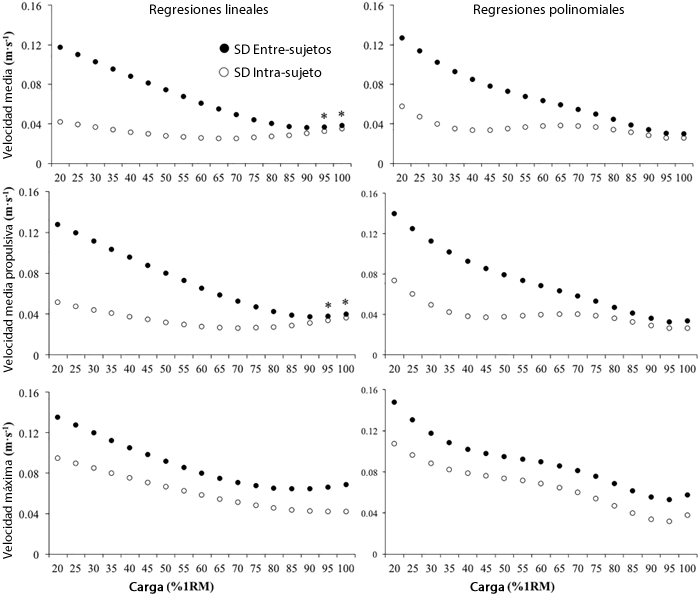
Figura 2. Desviación estándar (SD) intra-sujeto (círculo vacío) y entre-sujetos (círculo lleno) de la velocidad media (paneles superiores), velocidad media propulsiva (paneles centrales) y velocidad máxima (paneles inferiores) alcanzadas en cada porcentaje de una repetición máxima (%1RM) obtenida a partir de los modelos de regresión lineal (paneles izquierdos) y polinomial de segundo grado (paneles derechos). *Ratio de CV entre CVs intra-sujeto y entre-sujetos < 1,1.
https://doi.org/10.1371/journal.pone.0212085.g002

DISCUSIÓN

Este estudio fue diseñado para identificar la variable de velocidad y el modelo de regresión más apropiados para determinar la relación carga-velocidad durante el ejercicio prone bench pull con peso libre, así como para comparar la variabilidad entre- e intra-sujeto de los valores de velocidad alcanzados en cada %1RM. Los principales hallazgos del estudio revelaron que (I) las relaciones carga-velocidad generales e individuales eran altamente lineales, (II) la fiabilidad de la velocidad alcanzada en cada %1RM no difería sistemáticamente entre las variables de velocidad o entre los modelos de regresión, y (III) la variabilidad intra-sujeto de la velocidad alcanzada en cada %1RM era menor que la variabilidad entre-sujetos en todas las cargas submaximales (%1RM).

Dos estudios han examinado previamente la relación carga-velocidad durante el ejercicio prone bench pull realizado en una máquina Smith [14] o con pesos libres [17]. Tanto Sánchez-Medina et al. [14] utilizando un modelo de regresión polinomial y dos variables de velocidad (MV y MPV) (r2 = 0,95-0,96 y error estándar de estimación [SEE] = 5,31-5,90%1RM) como Loturco et al. utilizando un modelo de regresión lineal y tres variables de velocidad (MV, MPV y PV) (r2 = 0,90-0,91 y SEE = 6,27-6,56%1RM) recomendaron el uso de sus ecuaciones generales de relación carga-velocidad para estimar el %1RM. En consecuencia, de los resultados de los estudios actuales y anteriores se desprende que la relación carga-velocidad general podría obtenerse con una precisión similar a partir de las tres variables de velocidad diferentes (MV, MPV y PV) [12,14,17]. Además, basándose en los resultados del presente estudio, parece que la modelización de la relación carga-velocidad general durante el ejercicio bench pull con peso libre mediante un modelo de regresión polinomial no mejora sustancialmente la precisión en la estimación del %1RM en comparación con el uso de un modelo de regresión lineal. Sin embargo, es importante notar que debido a las limitaciones de las ecuaciones generales de relación carga-velocidad (para más detalles, ver García-Ramos y Jaric [21]), se recomienda la relación carga-velocidad individual para una prescripción más precisa de la carga relativa (%1RM) [7,22,23].

Apoyando nuestra primera hipótesis, la linealidad de las relaciones carga-velocidad individuales fue muy alta y no difirió significativamente entre las tres variables de velocidad. Este resultado difiere ligeramente de los resultados previamente informados por García-Ramos et al. [12] durante el ejercicio de press de banca en el que la MV mostró la mayor linealidad (r2 = 0,99), seguida por la MPV (r2 = 0,98), y finalmente la PV (r2 = 0,97). La alta linealidad de la relación carga-velocidad individual observada en el presente estudio, que coincide con los resultados obtenidos en otros ejercicios [7,12,13,23-25], proporciona evidencia adicional sobre la idoneidad del modelo de regresión lineal para evaluar la relación carga-velocidad individual durante los ejercicios básicos multiarticulares de entrenamiento de la fuerza. Sin embargo, debe tenerse en cuenta que a cargas muy ligeras (< 40%1RM) ni el modelo de regresión lineal ni el modelo de regresión polinomial fueron capaces de ajustar con precisión los valores de velocidad registrados. Este es un indicador de la baja capacidad de las ecuaciones generales de relación carga-velocidad para estimar cargas relativas bajas. Esta afirmación podría verse reforzada por las crecientes diferencias observadas entre la variabilidad entre-sujetos e intra-sujeto en los valores de velocidad cuando se reduce la carga relativa (ver Figura 2). Por lo tanto, es importante considerar que la precisión de las ecuaciones generales de relación carga-velocidad para estimar la carga relativa puede verse comprometida aún más a altas velocidades de movimiento.

Una de las novedades del presente estudio es que también comparamos la fiabilidad de los valores de velocidad alcanzados en cada %1RM entre las diferentes relaciones carga-velocidad individuales. Hasta donde sabemos, este tipo de comparación sólo se ha realizado para el ejercicio press de banca en el que la PV y el modelo de regresión lineal mostraron la mayor fiabilidad [12,16]. Sin embargo, rechazando nuestra segunda hipótesis, no se observaron diferencias sistemáticas en la fiabilidad de la relación carga-velocidad individual entre las variables de velocidad o entre los modelos de regresión. Por lo tanto, dado que la variabilidad entre-sujetos de la velocidad registrada en el test de 1RM fue menor para la MV que para la PV, es razonable proponer la MV como la variable de velocidad más apropiada. Debe tenerse en cuenta que cuando se levantan cargas pesadas (> 80%1RM) no hay diferencias entre los valores de MV y MPV [26]. En el presente estudio, la velocidad asociada en cada %1RM fue siempre similar para la MV y la MPV, ya que la barra no se frena intencionalmente durante el ejercicio bench pull, como es inevitable en el ejercicio de press de banca realizado con cargas ligeras [14,26]. Además, también debe tenerse en cuenta que la MV, pero no la MPV ni la PV, es una variable informada por todos los dispositivos de medición comerciales que han sido diseñados para medir la velocidad de movimiento durante el entrenamiento de la fuerza. Esto va acompañado de una mayor concordancia entre los dispositivos comerciales en la MV en comparación con los valores de la PV [27,28].

La tercera hipótesis de este estudio también fue confirmada, con la variabilidad intra-sujeto de la velocidad alcanzada en cada %1RM siendo generalmente más baja que la variabilidad entre-sujetos. Además, los significativos valores del ICC de la velocidad alcanzada con cargas relativas ligeras-moderadas (20-80% de 1RM) proporcionan apoyo adicional para el uso de relaciones carga-velocidad individuales sobre relaciones carga-velocidad generales. En línea con los resultados informados para el press de banca [16], los aumentos en la carga relativa se asociaron con reducciones en las diferencias entre la variabilidad entre-sujetos e intra-sujeto, así como con valores de ICC más bajos. Estos resultados indican que la velocidad asociada con cada %1RM es específica del sujeto, mientras que las diferencias entre-sujetos se acentúan a cargas relativas más bajas. De manera interesante, se observó una diferencia trivial y no significativa entre la variabilidad entre-sujetos e intra-sujeto para la MV registrada durante el test de 1RM. Este resultado presenta importantes aplicaciones prácticas para los profesionales, ya que podrían utilizar la MV promedio obtenida durante los tests de 1RM (es decir, 0,48 m·s-1) y, utilizando el valor de la MV registrado con varias cargas submaximales, predecir el valor de 1RM del prone bench pull con peso libre. La MV de al menos dos cargas submáximas debe modelarse mediante una regresión lineal y la 1RM se estimaría como la carga asociada a una MV de 0,48 m·s-1 [29]. Los estudios futuros deben procurar comparar la precisión de las relaciones carga-velocidad generales e individuales para predecir la 1RM durante los diferentes ejercicios de entrenamiento de la fuerza, así como determinar las combinaciones óptimas de cargas submaximales que deben considerarse para maximizar la precisión en la estimación de 1RM.

En conclusión, los resultados del presente estudio apoyan el uso de la MV y de un modelo de regresión lineal para la determinación fiable y precisa del perfil carga-velocidad durante el ejercicio prone bench pull con peso libre. Independientemente de la variable de velocidad y del modelo de regresión considerado, la variabilidad entre-sujetos de la velocidad alcanzada en las cargas ligeras-moderadas fue siempre considerablemente mayor que la variabilidad intra-sujeto, lo que sugiere que la relación carga-velocidad individual debería ser considerada para una prescripción más precisa de la carga relativa. Por otro lado, el bajo ICC y la variabilidad similar intra- y entre-sujetos de la MV obtenida durante el test de 1RM sugieren que se debe considerar una MV estándar de 1RM (0,48 m·s-1) para predecir la carga de 1RM de la MV registrada bajo varias cargas submaximales.

Agradecimientos

Nos gustaría agradecer a todos los deportistas que generosamente dieron su tiempo para participar en el estudio.

Referencias

1. Peart DJ, Balsalobre-Fernandez C, Shaw MP. (2018). Use of mobile applications to collect data in sport, health, and exercise science: A narrative review. J Strength Cond Res. 2018; in press. pmid:29176384

2. Dong J-G. (2016). The role of heart rate variability in sports physiology. Exp Ther Med. 2016;11: 1531–1536. pmid:27168768

3. Harris NK, Cronin J, Taylor KL, Boris J, Sheppard J. (2010). Understanding position transducer technology for strength and conditioning practitioners. Strength Cond J. 2010;32: 66–79.

4. Jovanonic M, Flanagan EP. (2014). Researched applications of velocity based strength training. J Aust Strength Cond. 2014;22: 58–69.

5. Mann J, Ivey P, Sayers S. (2015). Velocity-based training in football. Strength Cond J. 2015;37: 52–57.

6. González-Badillo JJ, Sánchez-Medina L. (2010). Movement velocity as a measure of loading intensity in resistance training. Int J Sports Med. 2010;31: 347–352. pmid:20180176

7. García-Ramos A, Pestaña-Melero FL, Pérez-Castilla A, Rojas FJ, Haff GG. (2018). Differences in the load-velocity profile between 4 bench press variants. Int J Sports Physiol Perform. 2018;13: 326–331. pmid:28714752

8. Sánchez-Medina L, González-Badillo JJ. (2011). Velocity loss as an indicator of neuromuscular fatigue during resistance training. Med Sci Sport Exerc. 2011;43: 1725–1734. pmid:21311352

9. González-Hernádez J, García-Ramos A, Capelo-Ramírez F, Castaño-Zambudio A, Marquez G, Boullosa D, et al. (2017). Mechanical, metabolic, and perceptual acute responses to different set configurations in full squat. J Strength Cond Res. 2017; in press. pmid:28700515

10. Weakley JJ, Wilson KM, Till K, Read DB, Darrall-Jones J, Roe G, et al. (2017). Visual feedback attenuates mean concentric barbell velocity loss, and improves motivation, competitiveness, and perceived workload in male adolescent athletes. J Strength Cond Res. 2017; in press. pmid:28704314

11. Randell AD, Cronin JB, Keogh JW, Gill ND, Pedersen MC. (2011). Effect of instantaneous performance feedback during 6 weeks of velocity-based resistance training on sport-specific performance tests. J Strength Cond Res. 2011;25: 87–93. pmid:21157389

12. García-Ramos A, Pestaña-Melero FL, Pérez-Castilla A, Rojas FJ, Haff GG. (2018). Mean velocity vs. mean propulsive velocity vs. peak velocity: which variable determines bench press relative load with higher reliability? J Strength Cond Res. 2018;32: 1273–1279. pmid:28557855

13. Conceição F, Fernandes J, Lewis M, Gonzaléz-Badillo JJ, Jimenéz-Reyes P. (2016). Movement velocity as a measure of exercise intensity in three lower limb exercises. J Sports Sci. 2016;34: 1099–1106. pmid:26395837

14. Sánchez-Medina L, González-Badillo JJ, Pérez CE, Pallarés JG. (2014). Velocity- and power-load relationships of the bench pull vs. bench press exercises. Int J Sports Med. 2014;35: 209–216. pmid:23900903

15. Pérez-Castilla A, García-Ramos A, Padial P, Morales-Artacho AJ, Feriche B. (2017). Load-velocity relationship in variations of the half-squat exercise: Influence of execution technique. J Strength Cond Res. 2017; in press. pmid:28885389

16. Pestana-Melero FL, Haff GGG, Rojas FJF, Pérez-Castilla A, García-Ramos A, Pestaña-Melero F, et al. (2017). Reliability of the load-velocity relationship obtained through linear and polynomial regression models to predict the one-repetition maximum load. J Appl Biomech. 2017;34: 184–190. pmid:29252060

17. Loturco I, Suchomel T, Kobal R, Arruda AFS, Guerriero A, Pereira LA, et al. (2018). Force-Velocity relationship in three different variations of prone row exercises. J Strength Cond Res. 2018; in press. pmid:29489715

18. Cormack SJ, Newton RU, McGuigan MR, Doyle TLA. (2008). Reliability of measures obtained during single and repeated countermovement jumps. Int J Sports Physiol Perform. 2008;3: 131–144. pmid:19208922

19. Fulton SK, Pyne D, Hopkins W, Burkett B. (2009). Variability and progression in competitive performance of Paralympic swimmers. J Sports Sci. 2009;27: 535–539. pmid:19219736

20. Hopkins W. Calculations for reliability (Excel spreedsheet). (2000). A New View of Statistics 2000. Accessed May 30, 2017. http://www.sportsci.org/resource/stats/relycalc.html.

21. Garcia-Ramos A, Jaric S. (2018). Two-Point Method: A quick and fatique-free procedure for assesment of muscle mechanical capacities and the one repetition maximum. Strength Cond J. 2018;40: 54–66.

22. Helms ER, Storey A, Cross MR, Brown SR, Lenetsky S, Ramsay H, et al. (2017). RPE and velocity relationships for the back squat, bench press, and deadlift in powerlifters. J Strength Cond Res. 2017;31: 292–297. pmid:27243918

23. Banyard HG, Nosaka K, Vernon AD, Haff GG. (2018). The reliability of individualized load-velocity profiles. Int J Sports Physiol Perform. 2018;13: 763–769. pmid:29140148

24. Jidovtseff B, Harris NK, Crielaard JM, Cronin JB. (2011). Using the load-velocity relationship for 1RM prediction. J Strength Cond Res. 2011;25: 267–270. pmid:19966589

25. Picerno P, Iannetta D, Comotto S, Donati M, Pecoraro F, Zok M, et al. (2016). 1RM prediction: a novel methodology based on the force-velocity and load-velocity relationships. Eur J Appl Physiol. 2016;116: 2035–2043. pmid:27577950

26. Sanchez-Medina L, Perez CE, Gonzalez-Badillo JJ. (2010). Importance of the propulsive phase in strength assessment. Int J Sports Med. 2010;31: 123–129. pmid:20222005

27. García-Ramos A, Pérez-Castilla A, Martín F. (2018). Reliability and concurrent validity of the velowin optoelectronic system to measure movement velocity during the free-weight back squat. Int J Sports Sci Coach. 2018; in press.

28. Fernandes J, Lamb K, Clark C, Moran J, Dury B, Garcia-Ramos A, et al. (2018). A comparison of the FitroDyne and GymAware rotary encoders for quantifying peak and mean velocity during traditional multi-jointed exercises. J Strength Cond Res. 2018; in press. pmid:30399117

29. García-Ramos A, Haff GG, Pestaña-Melero FL, Pérez-Castilla A, Rojas FJ, Balsalobre-Fernández C, et al. (2018). Feasibility of the 2-point method for determining the 1-repetition maximum in the bench press exercise. Int J Sports Physiol Perform. 2018;13: 474–481. pmid:28872384

Cita en PubliCE

Amador García-Ramos, David Ulloa-Díaz, Paola Barboza-González, Ángela Rodríguez-Perea, Darío Martínez-García, Mauricio Quidel-Catrilelbún, Francisco Guede-Rojas, Jesualdo Cuevas-Aburto, Danica Janicijevic Jonathon Weakley (2019). Evaluación del Perfil Carga-Velocidad en el Ejercicio Prone Bench Pull con Peso Libre mediante Diferentes Variables de Velocidad y Modelos de Regresión. .https://g-se.com/evaluacion-del-perfil-carga-velocidad-en-el-ejercicio-prone-bench-pull-con-peso-libre-mediante-diferentes-variables-de-velocidad-y-modelos-de-regresion-2525-sa-h5cc7390342c7b