Determinación No Invasiva de la Deformación del Cartílago de la Rodilla Durante el Salto
Nenad Filipovic1,3, Radun Vulovic1, Aleksandar Peulic1, Radivoje Radakovic1, Djordje Kosanic2, Branko Ristic1,41 Bioengineering Research and Development Center, BioIRC.
2 Sport Center "Mladost".
3 Faculty of Mechanical Engineering University of Kragujevac.
4 Medical Faculty Kragujevac, University of Kragujevac, Kragujevac, Serbia.
Resumen
El propósito de esta investigación fue utilizar una combinación de procesamiento de imágenes, mediciones de la fuerza y el modelo de elementos finitos para calcular la deformación del cartílago de la rodilla durante el salto. Un grupo de atletas profesionales realizaron saltos que fueron analizados utilizando una plataforma de fuerza y un sistema de videocámara de alta velocidad. El procesamiento de imágenes fue llevado a cabo en cada cuadro del video utilizando un algoritmo de reconocimiento de colores. Se utilizó un modelo simplificado de masas-resortes-amortiguadores para determinar la fuerza global y el momento de la rodilla. Se creo un programa a medida para que se ajustara a las características de acoplamiento. Los datos de la simulación computarizada fueron comparados con los datos experimentales de la fuerza de reacción promedio. Los resultados simulados fueron utilizados como datos de ingreso para el cálculo de elementos finitos de la deformación del cartílago de la rodilla de los atletas. Los resultados muestran que la distribución tridimensional de la deformación mecánica dentro del volumen del cartílago. La combinación de la tecnología de reconocimiento de imágenes, mediciones en plataforma de fuerza y el análisis de elementos finitos de la deformación del cartílago de la rodilla pueden utilizarse en el futuro como una herramienta no invasiva y efectiva para la predicción de lesiones durante actividades de saltos.
Palabras Clave: simulación, atletas, lesión
INTRODUCCION
El reciente desarrollo de nuevas tarjetas de captura de video, de la digitalización automática, la transformación en tiempo real y de programas de filtrado permite que puedan observarse datos cinemáticos y cinéticos en forma simultánea (Altmeyer et al., 1994; Ariel et al., 1997; Borelli, 1989). Estos datos pueden sincronizarse temporalmente de manera que los investigadores, entrenadores y atletas puedan evaluar en forma efectiva el rendimiento deportivo en diversas condiciones de competición. Además puede asistir a realizar los ajustes necesarios al entrenamiento (Braune et al., 1987; Finch et al., 1998; Plagenhoef, 1968). Las lesiones tendinosas son frecuentes en el deporte (Josza and Kannus, 1997) especialmente en los deportes explosivos donde las altas demandas de fuerza, velocidad y potencia son determinantes para un óptimo rendimiento.
Los atletas repetidamente se ven sujetos a un alto estrés durante el ejercicio lo que hace que la unión óseo-tendinosa, en el punto de mayor debilidad, sea susceptible a la lesión. La acumulación de microtraumas puede debilitar el entrecruzamiento de colágeno y finalmente resultar en la degeneración mucoidea del tendón (Khan et al., 1998). Como resultado, la determinación no invasiva de la deformación del cartílago de la rodilla puede ser una herramienta muy útil para la predicción de lesiones en la rodilla. En la investigación actual, para determinar la deformación del cartílago de la rodilla, se utiliza el análisis de imágenes de video conjuntamente con mediciones en plataformas de fuerza.
Los dispositivos para la adquisición de videos y el análisis sintético de secuencias de imágenes han influenciado significativamente la determinación de los algoritmos de seguimiento. La planificación cuidadosa de la adquisición de imágenes es crucial para el éxito del sistema propuesto. El seguimiento del movimiento de objetos pequeños puede ser bastante dificultoso y dependerá de diversos parámetros, especialmente de las condiciones ambientales y del tiempo de sistema para la adquisición de video. Si bien en el pasado se han desarrollado varios algoritmos de seguimiento, su robustez no ha sido claramente descrita en la literatura. Los métodos existentes pueden ser calificados como basados en hardware de alta tecnología o basados en algoritmos. En el primer grupo, se utiliza hardware de alta tecnología, i.e., video de alta calidad, múltiples cámaras con lentes de alta tecnología, computadoras potentes, una gran iluminación, etc. En dichos casos, los algoritmos aplicados no son muy sofisticados. Con frecuencia un simple dispositivo de seguimiento visual es suficiente (Pingali et al., 1998, 2000). El principal problema está en colocar y coordinar las múltiples cámaras o en visualizar los resultados del seguimiento de movimiento, por ejemplo en un ambiente virtual 3-D (Pingali et al., 1998, 2000). Sin embargo, se deben utilizar algoritmos especiales y muy sofisticados que sean capaces de resolver la tarea de compensar los deméritos. En el presente artículo, se propone un método intermedio entre los métodos previamente descritos. Por una parte se utilizó solo una cámara de alta velocidad, mientras que nuestro software de seguimiento del movimiento se basa en un algoritmo de un punto de referencia en movimiento (moving seed point). Se evitó la utilización de cámaras de alta velocidad para el cálculo de cinemáticas complejas en el seguimiento del movimiento. Con el uso de algunos algoritmos avanzados similares se pudo considerar el problema de la implementación de diversas condiciones experimentales.
En el presente estudio se utilizó un algoritmo combinado de seguimiento y procesamiento de imágenes para medir la cinemática y la dinámica de los atletas saltando sobre una plataforma de fuerza, conjuntamente con el cálculo numérico de la deformación del cartílago de la rodilla. En la siguiente sección se explican los procedimientos de medición de la fuerza, el algoritmo básico para el rastreo del objeto y el método numérico de elementos finitos para la deformación del cartílago.
METODOS
Medición de la Fuerza
El movimiento de la rodilla implica una serie de tres rotaciones (flexión/extensión, abducción/aducción e interna/externa) y tres traslaciones (anterior/posterior, superior/inferior y medial/lateral). Nuestro primer objetivo fue desarrollar un sistema computarizado para el seguimiento y análisis de las mediciones de la fuerza en la rodilla de los atletas durante el salto.
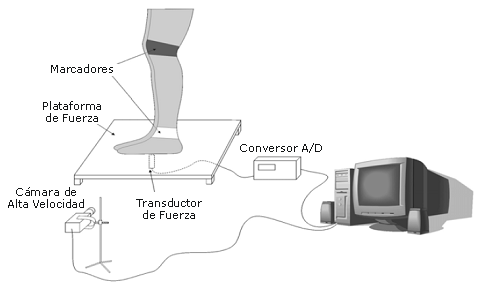
Figura 1. Equipamiento para la investigación experimental de la fuerza de impacto durante el salto y de la fuerza y el momento aplicados sobre la rodilla.
Las fuerzas de impacto registradas fueron utilizadas para calcular las fuerzas internas en el tobillo y la rodilla. Para esto se diseñó un dispositivo especial, un tipo de “plataforma de fuerza”, al que se le montó un transductor. Las mediciones de la fuerza fueron registradas completamente en paralelo con el análisis de video que controlado con un software específico (Figura 1). Luego de la adquisición de los datos experimentales, utilizamos nuestro software de video y procesamiento de imágenes para el análisis y la preparación de los datos para los cálculos numéricos. Los resultados de las mediciones llevadas a cabo en el tobillo y la rodilla fueron determinados separadamente en forma valores coordenados: coordenada X, coordenada Y, y fuerza de resistencia vertical F.
En cada salto individual se midieron las siguientes variables: (a) frecuencia de fotogramas, (b) tiempo total del experimento, (c) coordenadas bidimensionales de la rodilla y el tobillo en cada fotograma, (d) fuerzas medidas en la plataforma de fuerza para cada contacto, (e) número de saltos, y (f) velocidad máxima en el momento de la toma de contacto. El objetivo principal del presente experimento fue registrar simultáneamente datos de video y de la plataforma de fuerza. Se utilizaron cámaras de alta velocidad (Basler A602fc) en períodos de 10 segundos. Se guardó un archivo en formato AVI de aproximadamente 1.2 GB con las siguientes propiedades: 10 fps, 656×490 px, YUV 4:2:2 (16 bits/pixel promedio). Al mismo tiempo (en paralelo), se registraron las mediciones obtenidas con el transductor de fuerza a través de un puerto en serie. En cada caso, se registró el tiempo del sistema para la sincronización de las medidas.
Además, esta fase también incluyó la determinación de algunos parámetros necesarios para los siguientes cálculos numéricos: (a) separación de los saltos individuales, i.e., determinación de los tiempos de comienzo y fin de cada salto, (b) cálculo de la velocidad en el momento de la toma de contacto, (c) medición de la fuerza generada en el área de contacto, y (d) filtrado de las mediciones de la fuerza debido a la inercia de la plataforma de fuerza. Para cumplir con estos requisitos se establecieron algunos criterios. La mayoría fueron influenciados por nuestras impresiones visuales y conclusiones subjetivas acerca de los saltos y concordaron con los cambios en las mediciones de la fuerza. se definieron nueve fases del salto: (1) reposo, (2) preparación para el salto, (3) rebote (4), tiempo de vuelo, (5) caída, (6) toma de contacto con los dedos del pie, (7) toma de contacto con el talón, (8) preparación para el reposo y (9) reposo. El segundo criterio estuvo relacionado con la determinación de la velocidad al momento de la toma de contacto posterior al salto. Estos fueron los componentes horizontal y vertical de la velocidad durante la caída. En el momento en que el atleta toma contacto (sexta fase del salto), la velocidad alcanza su valor máximo y este valor fue utilizado para los subsiguientes cálculos numéricos. Este valor puede determinarse integrando las velocidades entre los subsiguientes fotogramas, comenzando con el fotograma en el cual este valor es cero. El fotograma inicial para este cálculo fue considerado como aquel obtenido en el instante final de la cuarta fase del salto, o el primer fotograma obtenido en el instante en que comenzaba la quinta fase del salto. Debido a que la aceleración durante la caída fue aproximadamente constante, la velocidad máxima en el momento en que el atleta tomaba contacto con la plataforma de fuerza fue calculada utilizando la siguiente ecuación:
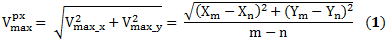
Donde n y m representan los índices de los fotogramas iniciales y finales, respectivamente. En el mismo sentido, los valores X e Y son las coordenadas del tobillo. La velocidad, de acuerdo con la ecuación (1) se expresó en [pixeles/número de fotogramas]. Para expresar la velocidad máxima en unidades del Sistema Internacional [m/s], el valor de Vmaxpx debe multiplicarse por el coeficiente K:
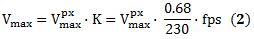
Donde 0.68 metros estuvo representado por 230 pixeles en fotogramas.
Algoritmo Propuesto para el Procesamiento de Imágenes y el Seguimiento del Movimiento
En esta sección se describe el problema del seguimiento de objetos en movimiento sobre una película registrada durante mediciones experimentales. El propósito no fue desarrollar un software que pudiera ser utilizado para el procesamiento de imágenes en tiempo real, sino desarrollar una aplicación que fuera simple, confiable, precisa, extensible y aun así poderosa para ajustarse a los requerimientos y desafíos impuestos por nuestro experimento.
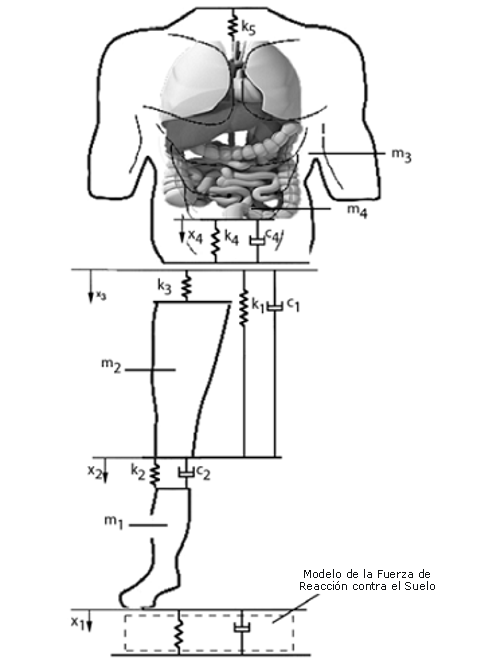
Figura 2. Modelo simplificado de masas-resortes-amortiguadores utilizando en la simulación computarizada. Los componentes del sistema dinámico presentados son: masa rígida (m1) y masa tambaleante (m2) del tren inferior, masa rígida (m3) y masa tambaleante (m4) del tren superior; resorte compresivo (k1) y amortiguador (c1) que conecta los cuerpos rígidos del tren superior e inferior; resorte (k3) y unidad resorte-amortiguador (k2, c2) que conectan la masa tambaleante del tren inferior con los cuerpos rígidos inferior y superior, resorte (k5) y unidad resorte-amortiguador (k4, c4) que conecta la masa tambaleante del tren superior con la masa rígida superior (Liu et al., 1998).
El seguimiento de objetos en movimiento siempre ha sido una tarea desafiante sin una única solución universal. Entre otras cosas, depende en gran medida de la calidad del material de video, i.e., depende indirectamente del hardware para la adquisición de imágenes y en forma global de las condiciones ambientales durante la grabación. Teniendo esto en mente, se decidió por buscar una solución que incluyera tanto hardware como software. Para el presente experimento se utilizó una cámara color de alta velocidad (Basler A602fc), 100 fps, y una resolución de 656×490 pixeles. Utilizando esta alta tasa de fotogramas se evitó la necesidad de desarrollar un algoritmo complejo para el seguimiento del movimiento. En esencia, existen dos algoritmos básicos para el seguimiento de movimiento: una aproximación de área y una aproximación diferencial (Mark et al., 2002). Estos algoritmos están basados en lo que se denomina “flujo óptico”, en donde las características de la imagen en los subsiguientes fotogramas tienen un cierto grado de relación entre sí. De hecho, “el movimiento puede ser caracterizado como una colección de desplazamientos en el plano de la imagen” (Mark et al., 2002). Este primer método se enfoca en buscar similitudes (e.g., pixeles) entre las intensidades de las regiones de la imagen. El segundo método se basa en la observación de los cambios diferenciales de los valores del pixel. Nuestro método fue más simple y algo diferente ya que se basó en hallar un nuevo “punto de muestreo” (seed point). A continuación se describirá como definir el punto de muestreo inicial y como seleccionar el área del objeto que debe ser seguido, así como también como comenzar todo el proceso de seguimiento.
Para realizar el seguimiento del movimiento del tobillo y la rodilla se decidió por colocar marcadores de color sobre estas articulaciones de manera tal que este color se distinguiera del color uniforme de fondo. De esta forma se evitaron los pasos relacionados con el mejoramiento de la imagen, debido a que ya poseíamos objetos de diferentes colores, de manera que el seguimiento pudiera ser llevado a cabo solo con esta característica. En este caso, se contó dos métodos para el seguimiento del movimiento. El primer método fue utilizado para realizar el seguimiento cuadro por cuadro de objetos de un único color y solo respecto de sus características de posición y color. El segundo método asumió la definición de AOI (área de interés) de la imagen para un determinado color. Debido a artefactos en la imagen (e.g., causado por el algoritmos de compresión de la imagen), se prefirió el primer método. Este fue más preciso que el segundo método y es el que se describe en el siguiente párrafo.
El paso inicial del algoritmo de seguimiento del movimiento fue la detección manual de un punto de muestreo y la definición de las tolerancias superiores e inferiores de los componentes del color (R, G, B) de este punto. Al definir las tolerancias para los componentes del color, en realidad se definió la selección de un área circundante al punto de muestreo, la cual estuvo compuesta por pixeles que compartían características similares (color), i.e., pixeles cuyo color estuviera dentro del rango de tolerancia definido para un determinado punto de muestreo. Se utilizó un algoritmo para definir la selección del área (A) en base a operaciones de vecindad (neighborhood operations) y se utilizó una pila como almacenamiento para los componentes conectados (i.e., pixeles). Es obvio que este algoritmo puede ser considerado como una especie de algoritmo de propagación (float-fill) (Glassner, 2001).
Modelo de Masas-Resortes-Amortiguadores
En el presente estudio se utilizó un modelo simplificado de masas-resortes-amortiguadores que se muestra en la Figura 2. Este modelo consiste en cuatro masas. El tren superior fue modelado utilizando dos masas, una representando su masa rígida, m3, y otra representando la masa tambaleante, m4. El muslo, la pierna y el pie de la extremidad de soporte también fueron modelados utilizando dos masas, una representando su masa rígida, m1 y otra representando su masa tambaleante, m2. La masa corporal total fue obtenida del sujeto. En el siguiente sistema de ecuaciones (ecuación 3) se describe la dinámica del sistema (Liu et al., 1998) que fue utilizada para el cálculo de la fuerza total y del momento del cartílago en la rodilla durante el salto.
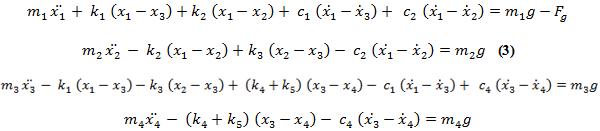
En la Ecuación 3, m1 representa la masa rígida del tren inferior y m2 la masa tambaleante, m3 representa la masa rígida del tren superior y m4 la masa tambaleante, k1 representa la compresión del resorte y c1 el amortiguador que conecta el tren superior y el tren inferior, k3 representa el resorte y k2-c2 es la unidad resorte-amortiguador que conecta la masa tambaleante del tren superior con las masas rígidas del tren superior e inferior, k5 representa el resorte y k4-c4 representa la unidad resorte-amortiguador que conecta la masa tambaleante del tren superior con la masa rígida del tren superior (Liu et al., 1998). Fg representa la fuerza vertical de contacto que fue definida como: Fg = Ac[axb1 + cxd1ve1] en donde Ac, a, b, c, d, y e son los parámetros para el modelo de reacción definido por la deformación del calzado durante el salto. En la Tabla 1 se muestran algunos de los parámetros para calzados blandos y duros.
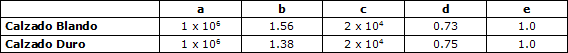
Tabla 1. Parámetros para el modelo de reacción contra el suelo.
Método de los Elementos Finitos para el Cálculo Numérico
El cartílago dentro de la rodilla fue considerado un cuerpo poroso y deformable lleno de fluidos que ocupan el volumen completo del poro. Las cantidades físicas para este análisis fueron: el desplazamiento del sólido u, la velocidad relativa del fluido con respecto al sólido (velocidad de Darcy) q, la presión del fluido p, la presión de hinchamiento pc y el potencial eléctrico. A continuación se describen las principales ecuaciones para el problema asociado. Primero, se consideró la ecuación de equilibrio para el sólido:
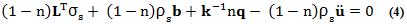
Donde σs representa el estrés en la fase sólida, n la porosidad, k la matriz de permeabilidad, ρs la densidad del sólido, b la fuerza corporal por unidad de masa, q la velocidad relativa del fluido y ü la aceleración del material sólido. El operador LT fue:
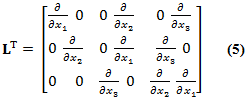
La ecuación de equilibrio de la fase sólida (sin acoplamiento electrocinético) fue:
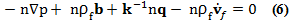
Donde p fue la presión de fluido en el poro, ρf representa la densidad del fluido y vf la aceleración del fluido. Esta ecuación también es conocida como la ley general de Darcy. Ambas ecuaciones de equilibrio fueron escritas por unidad de volumen de la mezcla. La combinación de las Ecuaciones (4) y (6) produjo la siguiente ecuación:
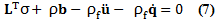
Donde σ fue el estrés total expresado en términos de σs y p como:
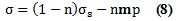
Y σ = (1-n) σs + nσf representa la densidad de la mezcla. Aquí m fue un vector constante definido como mT = {1 1 1 0 0 0} para indicar el componente de presión que contribuye solamente al estrés normal. También se tuvo en cuenta la que la presión tiene signo positivo en la compresión, a la vez que el estrés de tensión y el impacto también fueron considerados positivos. En el siguiente análisis se empleó el estrés efectivo, σ, definido como:
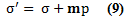
El cual es relevante para las relaciones constitutivas del sólido. Utilizando la definición de velocidad relativa q, como el volumen de fluido que pasa por unidad de tiempo a través de una unidad de área (velocidad de Darcy),
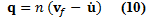
Transformamos la ecuación (6) en:
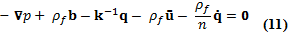
La ecuación de continuidad final utilizando la ley constitutiva de elásticos y la incompresibilidad de fluidos fue dada en la forma (Kojic, et al., 2001):
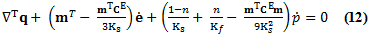
El sistema de ecuaciones resultante FE fue resuelto incrementalmente (Kojic et al., 2001) con el gradiente de tiempo Δt. Se impuso la condición de que las ecuaciones de equilibrio se satisfacen al final de cada gradiente de tiempo (t + Δt). Por lo tanto, se derivó el siguiente sistema de ecuaciones:
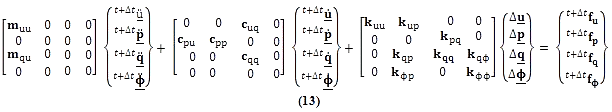
Donde fu, fp, fg y fΦ son las fuerzas en las ecuaciones de equilibrio para el desplazamiento, la presión, la velocidad de fluido y el potencial eléctrico respectivamente; y muu y mqu son los términos de masa en la matriz de masa.
RESULTADOS
El objetivo de este estudio fue calcular la deformación del cartílago de la rodilla en base a un modelo de la rodilla del sujeto y al análisis biomecánico del salto. En la Figura 3 se presentan los valores globales de las fuerzas impuestas sobre la articulación de la rodilla. Si bien existen diferentes fuerzas actuando sobre la rodilla, para simplificar hemos considerado solo una fuerza dimensional determinada por el sistema dinámico en la Ecuación 3. El cuadro de diálogo del software desarrollado para la captura de movimiento del sujeto se muestra en la Figura 4.
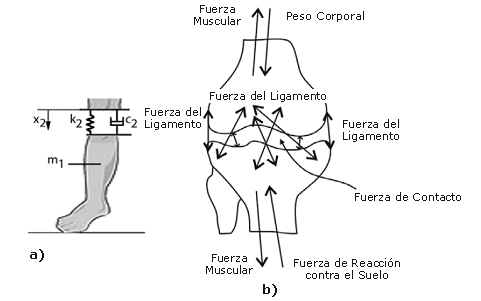
Figura 3. Aproximación esquemática de las fuerzas actuantes sobre la rodilla. (a) Sistema dinámico de la deformación de la rodilla durante el salto; (b) descripción de las fuerzas dentro de la articulación de la rodilla.
El trazado de una línea a lo largo de la extremidad inferior del sujeto en la Figura 4 permitió el seguimiento de un segmento rígido con dos puntos o articulaciones. La articulación superior correspondió al movimiento de la rodilla y la fuerza aplicada sobre este punto fue de particular interés para la determinación de la deformación del cartílago. En la Figura 5 se muestra la fuerza medida con la plataforma de fuerza. Utilizando estos resultados experimentales se calculó la fuerza y el movimiento sobre el cartílago de la rodilla, tal como se describe en la segunda sección de los Métodos. La articulación de la rodilla fue analizada mediante transducción electrocinética en un material cargado, homogéneo, isotrópico e hidratado. En el análisis primero se utilizaron las constantes del material publicadas por Frank et al (1987a, 1987b). Posteriormente, se ajustaron los valores de las constantes del material a los datos del experimento empleando nuestras soluciones numéricas. Los resultados del ajuste se muestran en la Figura 6 y los parámetros básicos de ajuste se muestran en la Tabla 2.
Utilizando la aproximación de Frank et al (1987a, 1987b), se asumió que el fluido y el sólido eran incompresibles, y la compresión del tejido fue tomada como una constante. El modulo de elasticidad de Young fue E = 4.5 × 103 [N/m2] y Kf = 2.2 × 103. La fuerza pico promedio fue determinada a partir de la fuerza de reacción contra el suelo medida en la plataforma de fuerza (Figuras 5 y 6) resolviendo un sistema un sistema de ecuaciones unidimensional (Ecuación 3). Los resultados de la deformación del cartílago para una fuerza pico promedio de 166 N se presentan en la Figura 7.
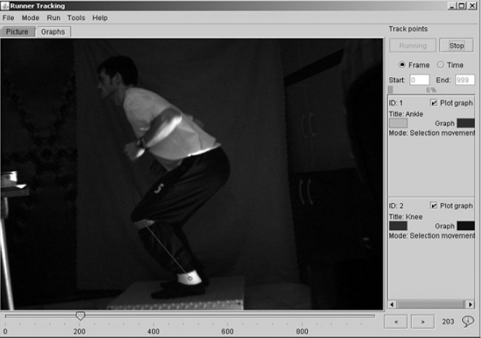
Figura 4. Captura de imágen en 3D y mediciones de la plataforma de fuerza durante la ejecución de un salto.
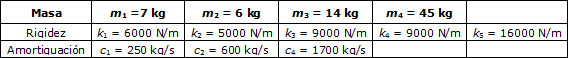
Tabla 2. Parámetros ajustados del sistema dinámico.
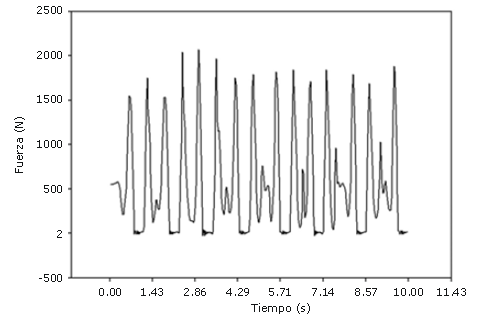
Figura 5. Fuerza versus tiempo durante la fase de evaluación del salto.
DISCUSION
El rango estimado de fuerza pico se correspondió con los resultados de algunos estudios previos en los que se determinó la fuerza vertical dentro de la rodilla de humanos (Lee et al., 2004). La aproximación unidimensional del modelo dinámico de la Ecuación 3 parece ser razonable. Los datos geométricos del modelo del cartílago fueron parametrizados de acuerdo con el modelo de la rodilla publicado en la literatura (Fernandez y Pandy, 2006). Los resultados iniciales para la deformación del cartílago también estuvieron dentro del rango observado en estudios previos (Bei y Fregly, 2004). Este fue considerado un buen punto de partida para la determinación no invasiva del estrés y la deformación del cartílago de la rodilla así como también de otras partes del modelo de la rodilla.
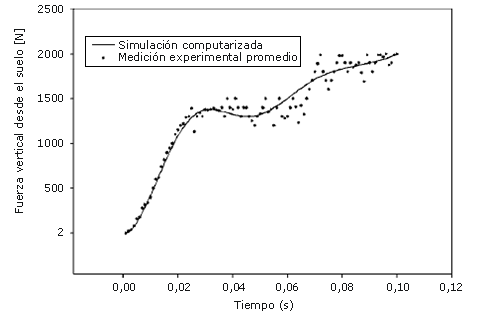
Figura 6. Ajuste de los parámetros dinámicos para la fuerza de contacto contra el suelo Fg (ver Ecuación 3).
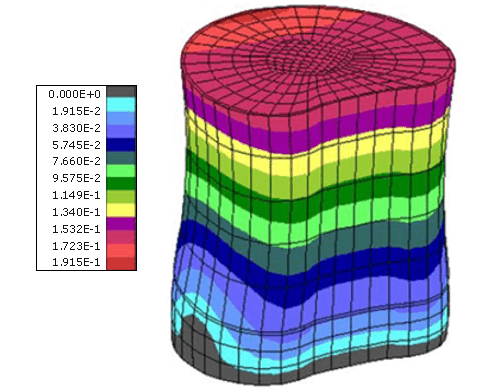
Figura 7. Deformación del cartílago para una fuerza pico de 166 N durante un salto en plataforma de fuerza. las unidades en la paleta de color para la deformación están en centímetros.
CONCLUSIONES
En el presente estudio se ha utilizado la combinación de un algoritmo de seguimiento para el procesamiento de imágenes y la medición de la cinemática y la dinámica del salto sobre una plataforma de fuerza. Se desarrolló un algoritmo simplificado para el modelo de resortes-amortiguadores y masas para la determinación de la fuerza y el momento aplicados sobre el cartílago dentro de la rodilla. Se implementó el cálculo de elementos finitos para la deformación del cartílago durante el movimiento de la rodilla.
Estas técnicas experimentales y computacionales podrían ser una buena plataforma para la futura evaluación de los atletas. Mediante la utilización de esta metodología los entrenadores podrían evaluar de forma efectiva el rendimiento deportivo bajo diferentes condiciones competitivas y posiblemente evitar lesiones durante el entrenamiento. El siguiente paso sería incluir el control neuromuscular del salto. Además, se debería considerar el mecanismo causal de la rodilla del saltador en el deporte y los posibles factores de riesgo para una mayor comprensión de los mismos.
Puntos Clave
- Aun cuando existen diversos modelos matemáticos para la distribución de la fuerza durante la carrera o el salto (Liu et al., 1998), para nuestro conocimiento no existe un enfoque interdisciplinario en donde se haya empleado el procesamiento de imágenes, el modelo de elementos finitos y una plataforma de fuerza experimental.
- El propósito de este estudio fue explorar la deformación no invasiva del cartílago de la rodilla durante el salto sobre una plataforma de fuerza.
- Se desarrolló un algoritmo de imágenes y un software original así como también un modelo matemático complejo utilizando la potencia computacional de alto rendimiento del modelo de elementos finitos conjuntamente con un modelo dinámico unidimensional.
- Los resultados iniciales mostraron la deformación del cartílago de la rodilla y los estudios futuros deberían enfocarse en el desarrollo de una metodología más precisa para la determinación de la distribución del estrés y el impacto sufrido por el cartílago de la rodilla durante la fase de entrenamiento en deportistas.
Agradecimientos
Este estudio fue subvencionado por el Ministerio de Ciencia de Serbia, TR12007, OI144028.
Dirección para el envío de correspondencia: Nenad Filipovic. Faculty of Mechanical Engineering, University of Kragujevac, Sestre Janjica 6, 34000 Kragujevac, Serbia. (fica@kg.ac.rs).
Referencias
1. Altmeyer, L., Bartonietz, K. and Krieger, D (1994). Technique and training: the discus throw. Track & Field Quarterly Review 994(3), 33-34
2. Ariel, G., Finch, A. and Penny, A (1997). Biomechanical analysis of discus throwing at the 1996 Atlanta Olympic Games. Biomechanics in Sports XV. 365-371
3. Borelli, K.D (1989). De motu animalium.pais prima 1680. Springer Verlag, Berlin
4. Braune, W. and Fischer, O (1987). The human gait. Springer Verlag, Berlin
5. Fernandez, J.W. and Pandy, M.G (2006). Integrating modelling and experiments to assess dynamic musculoskeletal function in humans. Experimental Physiology 991, 371-382
6. Finch, A., Ariel, G. and Penny, A (1998). Kinematic comparison of the best and worst of the top mens discus performers at the 1996 Atlanta Olympic Games. International Symposium on Biomechanics in Sports I, 93-96
7. Frank, E.H. and Grodzinsky, AJ (1987). Cartilage electromechanics-I. Electrokinetic transduction and the effects of electrolyte pH and ionic strength. Journal of Biomechanics 20, 615-627
8. Frank, E.H. and Grodzinsky, AJ (1987). Cartilage electromechanics-II. A continuum model of cartilage electrokinetics and correlation with experiments. Journal of Biomechanic 20, 629-639
9. Glassner, A (2001). "Fill Er Up!". IEEE Computer Graphics and Applications. 21(1), 78-85
10. Khan, K.M., Maffulli, N., Coleman, B.D., Cook, J.L. Taunton, J.E (1998). Patellar tendinopathy: some aspects of basic science and clinical management. British Journal of Sports Medicine 332, 346-355
11. Kojic, M., Filipovic, N., Mijailovic, S (2001). A large strain finite element analysis of cartilage deformation with electrokinetic coupling. Computer Methods in Applied Mechanics and Engineering 190, 2447-2464
12. Liu, W., Benno, M. and Nigg, A (1998). Mechanical model to determine the influence of masses and mass distribution on the impact force during running. Journal of Biomechanics 33, 219-224
13. Mark, S., Nixon, Alberto, S. Aguado (2002). Feature Extraction and Image Processing. Newnes
14. Pingali, G.S., Jean, Y. and Carlbom, I (1998). Real time tracking for enhanced tennis broadcasts. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Computer Society. 260-265
15. Pingali, G.S. Opalach, A. and Jean, Y (2000). Ball tracking and virtual replays for innovative tennis broadcasts. IEEE International Conference on Pattern Recognition 4, 152-156
16. Plagenhoef, S (1968). Computer programs for obtaining kinetic data on human movement. Journal of Biomechanics 1, 221-234
17. Lee, W., Zhang, M., Jia, X.,Cheung, J (2004). Finite Element Modeling of the Contact Interface Between Trans-Tibial Residual Limb and Prosthetic Socket. Medical Engineering & Physics 226(8), 655-662
18. Bei, Y. and Fregly, B (2004). Multibody dynamic simulation of knee contact mechanics. Medical Engineering & Physics 26(9), 777-789
Cita Original
Nenad Filipovic, Radun Vulovic, Aleksandar Peulic, Radivoje Radakovic, Djordje Kosanic and Branko Ristic. Noninvasive Determination of Knee Cartilage Deformation during Jumping. Journal of Sports Science and Medicine (2009) 8, 584 - 590.
Cita en PubliCE
Nenad Filipovic, Radun Vulovic, Aleksandar Peulic, Radivoje Radakovic, Djordje Kosanic Branko Ristic (2014). Determinación No Invasiva de la Deformación del Cartílago de la Rodilla Durante el Salto. .https://g-se.com/determinacion-no-invasiva-de-la-deformacion-del-cartilago-de-la-rodilla-durante-el-salto-1226-sa-557cfb271d94b4
