Construcción de Modelos para la Interacción en el Deporte: Fase Relativa y Correlaciones de Movimiento
Martin Lames11 Institute for Sports Science, Augsburg University, Bavaria, Germany.
Resumen
La construcción de modelos en el deporte debería mantener la característica constitutiva de este grupo de deportes, el proceso de interacción dinámica entre dos oponentes o grupo de oponentes. Para aquellos deportes individuales en donde los oponentes están separados por una red o en donde una pelota rebota contra una pared, se sugiere que la fase relativa describe la interacción posicional entre los dos jugadores. Se examinaron 30 peloteos en tenis y se calculó la fase relativa mediante la transformación de Hilbert a partir de series temporales de desplazamiento lateral y de trayectorias en la cancha. Los resultados mostraron que la fase relativa indica algunos aspectos de la interacción táctica en el tenis. A un nivel más abstracto, se estudió la interacción entre dos equipos de handbol examinando la relación de los dos procesos de anotación. Cada proceso puede ser concebido como un algoritmo simple (o camino aleatorio). El promedio de las probabilidades de anotación indican algo así como una fortaleza momentánea. Una correlación móvil (duración = 20 posesiones del balón) describe la relación momentánea entre las fortalezas de los equipos. Se ha hallado evidencia de que esta correlación es altamente dependiente del tiempo, y en casi cada uno de los 40 partidos que examinamos hemos hallado fases con una relación positiva significativa así como también con una relación negativa significativa. Esto subraya la importancia de poseer una visión dinámica de la interacción en estos deportes.
Palabras Clave: juegos deportivos, construcción de modelos, fase relativa, camino aleatorio
INTRODUCCION
Los juegos deportivos pueden definirse como aquellos deportes en donde dos oponentes (equipos, dobles o singles) tratan de alcanzar su meta y evitar que el oponente alcance la suya (Lames, 1991). Esto constituye un proceso de interacción, y el rendimiento observable es mas el resultado emergente de este proceso de interacción que la de las destrezas y habilidades de los oponentes. La naturaleza de los juegos deportivos también implica que este proceso de interacción es dinámico. Este proceso cambia durante el juego debido a la búsqueda permanente de un comportamiento exitoso, debido a consideraciones estratégicas que dependen, por ejemplo, del resultado o debido a la reacción impuesta por una acción del oponente. Esto contrasta marcadamente con otros deportes tales como los 100 m lisos o la maratón, donde el rendimiento es mayormente determinado por las destrezas y habilidades (en su mayoría constantes) de los atletas.
Si se acepta esta noción de los juegos deportivos como un proceso de interacción dinámica se podrían extraer dos consecuencias importantes. Primero, algunos de los métodos tradicionales para el análisis del rendimiento en las ciencias del deporte se volverían dudosos. Por ejemplo, la búsqueda de normas de comportamiento sería un esfuerzo fútil ya que el comportamiento cambia dramáticamente y emerge a partir del encuentro singular de dos oponentes. Asimismo, la valoración de las destrezas individuales en los juegos deportivos sería un problema ya que las mediciones utilizadas suman las frecuencias de comportamientos observados y no respetan la singularidad y dinámica de un proceso de interacción. La segunda consecuencia es que esta noción estimula la búsqueda de nuevos modelos que sean capaces de describir las propiedades cruciales de los juegos deportivos, interacción y dinámica.
En este artículo se describen dos enfoques que sortean los desafíos descritos previamente a partir de diferentes perspectivas. Primero, la interacción posicional para aquellos deportes individuales en donde los oponentes están separados por una red o en donde una pelota rebota contra una pared se describe por la fase relativa entre sus trayectorias. El segundo enfoque utiliza el concepto de camino aleatorio para valorar la fortaleza dinámica de dos equipos en los juegos de invasión y estudia la interacción entre dos procesos mediante correlaciones móviles.
FASES RELATIVAS EN EL TENIS
La idea de describir los movimientos de dos jugadores con sus fases relativas fue introducida en primer lugar por McGarry et al (1999) para el squash. Estos investigadores fueron influenciados por la interpretación de que los jugadores se mueven de la misma manera que lo hace una pareja que danza. Ciertamente, otra fuente de esta idea fue la aplicación exitosa de las fases relativas para describir patrones coordinados en las ciencias del movimiento (Haken et al., 1985; Kelso, 1995). McGarry et al (1999) examinaron la distancia absoluta de los jugadores a partir de la mitad de la cancha y hallaron un comportamiento predominantemente anti-fase. Palut y Zanone (2005) calcularon la fase relativa por primera vez utilizando la transformación de Hilbert. Estos investigadores utilizaron la distancia lateral a partir de la mitad de la cancha de tenis y también hallaron que en la mayor parte del tiempo los jugadores mostraban un comportamiento anti-fase, pero también hallaron que los valores en-fase de las fases relativas mostraron un máximo relativo.
Nuestras investigaciones también fueron llevadas a cabo con jugadores de tenis. En estos estudios nos concentramos en los problemas metodológicos y evaluamos el significado de los diferentes valores de la fase relativa para el estatus del juego.
¿Por qué la fase relativa es un enfoque prometedor para describir las interacciones espaciales en aquellos juegos individuales en donde los oponentes están separados por una red o en donde una pelota rebota contra una pared? Desde el punto de vista de los sistemas, los movimientos en el tenis pueden ser percibidos como los movimientos de dos subsistemas, los jugadores. Estos subsistemas están fuertemente acoplados por la naturaleza del juego ya que hay un intercambio de “golpes”. Mientras uno de los jugadores golpea la pelota, el otro trata de quedar en una posición “neutral” a partir de la cual tenga las mayores oportunidades de arribar en tiempo para dar su siguiente golpe. En el instante en que el jugador reconoce la dirección de la pelota se mueve al lugar de contacto, mientras que el otro jugador se mueve a su posición “neutral”. La Figura 1 muestra un peloteo ideal con golpes de derecha y un peloteo cruzado con las correspondientes posiciones.
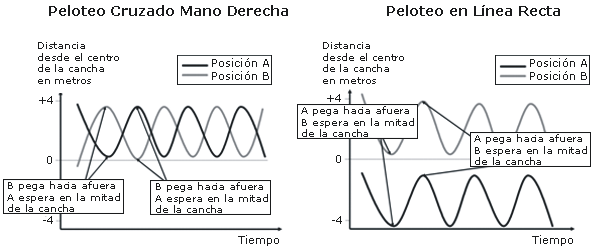
Figura 1. Trayectorias ideales de desplazamiento lateral durante un
peloteo cruzado y durante un peloteo en línea recta en tenis. La fase relativa
es constante en ambos caso, anti-fase (180º, izquierda) y en-fase (0º, derecha).
Una hipótesis muy interesante desde un punto de vista práctico es la relación entre la fase relativa y el estado del peloteo. Se podría asumir que una fase relativamente estable indica un juego estable en el cual ninguno de los jugadores tiene problemas para llegar justo a tiempo para dar su golpe. No obstante, la naturaleza del tenis demanda colocar los golpes con velocidad y precisión para presionar al oponente y en definitiva ganar el punto. Esto debería resultar en una perturbación de la fase relativa. Por lo tanto, la hipótesis es que en una fase estable del peloteo, la fase relativa es estable, pero en la fase final, cuando se anota un punto ganador o el oponente es forzado a cometer un error, la fase relativa se vuelve inestable. Si se pudiera probar esta hipótesis entonces podríamos determinar la presión creada durante un peloteo, lo que a su vez se convertiría en un valioso instrumento para el análisis práctico.
Nosotros examinamos 30 peloteos entre jugadores de elite, registrados durante la televisación de los torneos de Gran Slam (París y Melbourne). Los peloteos fueron seleccionados si tenían una duración considerable y si eran jugados y finalizados en la línea de fondo. De estos 30, 18 fueron jugados por tenistas femeninos. Las posiciones de los jugadores fueron obtenidas mediante métodos de detección de imágenes provistos por la Facultad de Ciencias Informáticas de la Universidad Tecnológica de Munich. Las fases relativas fueron calculadas a partir de series temporales suavizadas (filtrado a 1Hz) de las posiciones de los dos jugadores. Para los cálculos se utilizó el algoritmo de la transformación de Hilbert (MatLab). Este procedimiento es muy conocido en Teoría de Señales y permite calcular una fase relativa continua, lo cual fue primordial ya que contábamos con pocos golpes por peloteo (Pikovsky et al., 2001).
El primer aspecto metodológico que tratamos fue cual serían los datos óptimos necesarios para calcular la fase relativa. Hallamos que los desplazamientos laterales (ver Figura 2) proveen una buena representación del comportamiento en la cancha, pero tienen ciertas debilidades en su estructura de fase. Esto se debe al hecho de que incluso en los peloteos realizados desde la línea de fondo los jugadores se mueven también perpendicularmente a esta línea en forma considerable. Como resultado las fases relativas a veces muestran características que son difíciles de interpretar si solo se quieren tener en cuenta los desplazamientos laterales. El final del peloteo es “anunciado” por el cambio en la fase relativa desde una posición en-fase a una posición anti-fase.
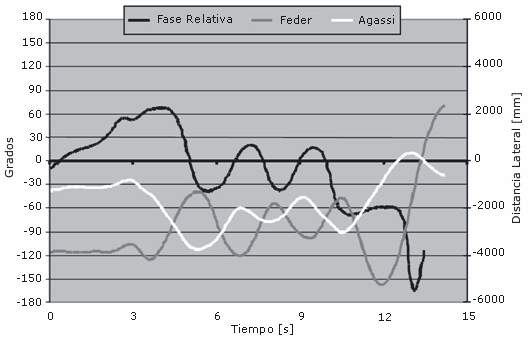
Figura 2. Desplazamiento lateral y su fase relativa entre dos jugadores
de sexo masculino.
Como una alternativa, evaluamos las trayectorias de los jugadores dentro de la cancha medición a medición (25 Hz). En realidad estos son datos de velocidad y las fases relativas ahora informan acerca de la relación entre la fase y la velocidad de movimiento, independientemente de las posiciones en la cancha. Con estos datos comúnmente obtenemos claros resultados acerca de las fases relativas pero no podemos tener muy en claro que es lo que está sucediendo en la cancha (ver Figura 3). Como resultado, sugerimos la utilización del análisis de los desplazamientos laterales así como también de las trayectorias bidimensionales en la cancha.
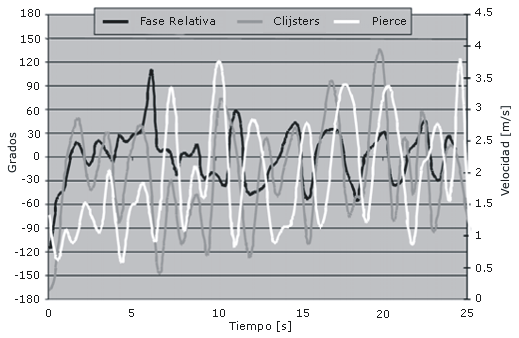
Figura 3. Velocidad de dos jugadoras de tenis y sus fases relativas
respecto de los datos de la velocidad.
La estructura cíclica de las series temporales es evidente, el peloteo finaliza con un error no forzado o con cambio no “anunciado” en la fase relativa que fluctúa alrededor de la posición en-fase durante el peloteo.
Los resultados concernientes a la distribución de las fases relativas muestran que con los datos de velocidad obtenemos un pico en la distribución que indica la dominancia de la posición en-fase. Esto se debe al hecho el peloteo sincroniza a los jugadores en el sentido de que se alternan entre dos estados: de baja velocidad mientras un jugador golpea la pelota y el otro se orienta para el siguiente golpe, y de alta velocidad mientras un jugador se aproxima a la pelota para realizar el golpe y el otro vuelve hacia la posición neutral. Esto concuerda con los hallazgos de Palut y Zanone (2005)
La siguiente tarea será vincular la fase relativa al comportamiento táctico en la cancha. Una forma de realizar esto podría ser examinar cuidadosamente una mayor cantidad de peloteos entre jugadores de clase mundial; no obstante se podría instruir a los jugadores de nivel nacional a que exhiban los comportamientos que deseamos de acuerdo con nuestras instrucciones y estudiar el comportamiento provocado de la fase relativa.
MODELO DEL CAMINO ALEATORIO EN EL HANDBOL
El desarrollo de la marcación de puntos durante un partido de handbol puede percibirse como dos caminos aleatorios entrelazados. Cada equipo tiene una probabilidad p de anotar cuando se encuentra en posesión del balón, P(1) = p, y una probabilidad q = 1 de no anotar, P(0) = q. La Figura 4 (Gráfico A) muestra estos dos caminos aleatorios en un juego del Campeonato Mundial del 2001 entre Alemania y Croacia. Parece obvio que los procesos son dinámicos, tenemos fases en las cuales cada posesión del balón deriva en una anotación pero también observamos períodos en los cuales no hay anotaciones. El rendimiento a nivel local puede describirse mediante promedios móviles del marcador. En la Figura 4 (Gráfico B) se muestran los promedios móviles en períodos de 4 min para cada equipo. Esto refleja algo así como la fortaleza momentánea de cada equipo y nos brinda información acerca de cómo interactúan ambos equipos.
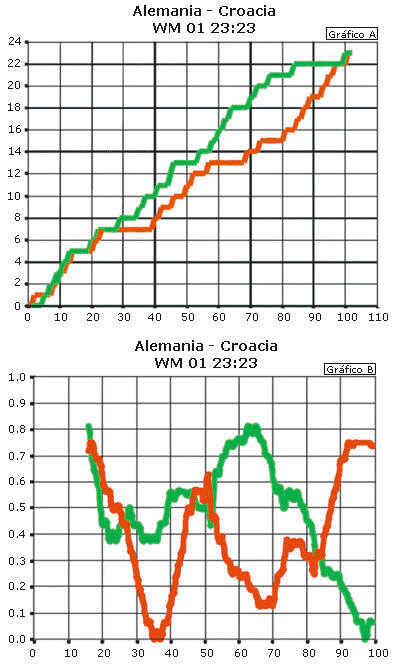
Figura 4. Gráfico A: desarrollo del marcador
durante un partido de handbol.Gráfico B: promedio móvil
de la probabilidad de anotación.
Existe evidencia que respalda la hipótesis de que la tasa de anotación de un equipo es independiente de la del otro equipo, pero también observamos fases que parecen tener una fuerte dependencia. Asimismo, a veces las probabilidades momentáneas de anotación parecen estar negativamente correlacionadas (uno de los equipos anota mucho cuando el otro anota poco y viceversa; esto puede observarse en la mitad y al final del juego), pero a veces hay una correlación positiva (uno de los equipos se desempeña bien cuando lo hace el otro, esto puede observarse al inicio del juego).
Esto deriva en la idea de calcular correlaciones móviles para estudiar la relación entre dos procesos de anotación. La Figura 5 muestra que hay fases con correlaciones positivas y negativas significativas. Este comportamiento fue característico en la mayoría de los 30 partidos examinados hasta ahora.
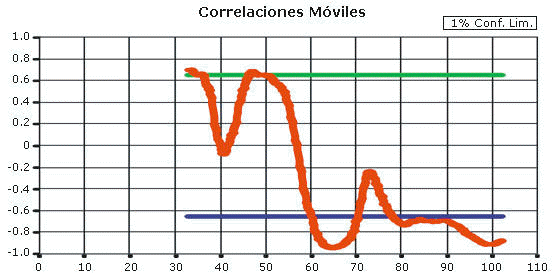
Figura 5. Correlaciones móviles con una duración de 20 posesiones entre
las probabilidades de anotación de la Figura 4 Gráfico B.
DISCUSION
La construcción de modelos de la interacción posicional entre jugadores de tenis mediante fases relativas promete revelar importantes características de la naturaleza del juego. Los aspectos centrales del comportamiento se encuentran descritos por las fases relativas. Una limitación de esto yace en el hecho de que las fases relativas solo son aptas para peloteos de larga duración en donde los jugadores tratan de presionar a través de las posiciones, mientras que la obtención de puntos a través del saque o por errores no forzados no tienen impacto en las fases relativas. Una perspectiva interesante es la descripción de otros deportes individuales en donde los oponentes están separados por una red o en donde una pelota rebota contra una pared, tales como el squash y el badminton, mediante la utilización de fases relativas.
La examinación de los procesos de anotación como caminos aleatorios en el handbol puede darnos un mayor entendimiento tanto teórico como práctico. Para los teóricos es fascinante estudiar las dinámicas de interacción durante un juego. Para los entrenadores puede ser interesante identificar fases exitosas y menos exitosas durante un juego como punto de partida para un análisis práctico del juego.
CONCLUSIONES
La construcción de modelos de interacción en los juegos deportivos es un desafío para la ciencia de los deportes. Con los dos modelos aquí propuestos se pueden analizar algunos aspectos de la interacción: la interacción espacial en deportes individuales en donde los oponentes están separados por una red o en donde una pelota rebota contra una pared mediante la utilización de fases relativas y los procesos de anotación en los deportes de conjunto mediante un modelo estocástico.
Puntos Clave
- Juegos deportivos
- Modelos matemáticos
- Fases relativas
- Caminos aleatorios
Agradecimientos
Quisiera agradecer a mi estudiante Florian Walter por sus cálculos de las fases relativas con el programa MatLab.
Referencias
1. Haken, H., Kelso, J.A.S. and Bunz, H (1985). A theoretical model of phase transitions in human hand movements. Biological Cybernetics 551, 347-356
2. Kelso, J.A.S (1995). Dynamic patterns. the self-organization of Brain and Behavior. Cambridge, Mass.: MIT-Press
3. Lames, M (1991). Leistungsdiagnostik durch Computersimulation: Ein Beitrag zur Theorie der Sportspiele am Beispiel Tennis. Frankfurt, Thun: Harry Deutsch
4. McGarry, T., Anderson, D.I., Wallace, S.A., Hughes, M.D. and Franks, I.M (2002). Sport competition as a dynamical self-organizing system. Journal of Sport Sciences 220, 771-781
5. McGarry, T., Khan, M.A. and Franks, I.M (1999). On the presence and absence of behavioural traits in sport: an example from championship squash match-play. Journal of Sport Sciences 117, 297-311
6. Pikovsky, A., Rosenblum, M. and Kurths, J (2001). Synchronization: A universal concept in nonlinear sciences. Cambridge: University Press
7. Palut, Y. and Zanone, P.-S (2005). A dynamical analysis of tennis player is motion: Concepts and data. Journal of Sports Science 23, 1021-1032
Cita Original
Martin Lames. Modelling the Interaction in Game Sports - Relative Phase and Moving Correlations. Journal of Sports Science and Medicine (2006) 5, 556 - 560
Cita en PubliCE
Martin Lames (2006). Construcción de Modelos para la Interacción en el Deporte: Fase Relativa y Correlaciones de Movimiento. .https://g-se.com/construccion-de-modelos-para-la-interaccion-en-el-deporte-fase-relativa-y-correlaciones-de-movimiento-929-sa-d57cfb2719f6bb
